Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.4 - Ex. 45
Calcule as forças nos elementos , e da treliça carregada, sem calcular primeiro a força em qualquer outro elemento.
Passo 1
Vamos olhar para um seção que acaba nos pontos e . É preciso lembrar que só consideramos as forças externas a esse sistema que vamos definir:
Nesse caso, em teremos duas forças: uma igual ao peso da carga, que aponta na vertical para baixo, e uma com a metade do peso da carga, já que a polia móvel divide a força em dois, apontado na horizontal para a direita.
E agora vamos pensar em . Nesse caso temos as duas componentes da força . Na vertical para baixo temos , e na horizontal para baixo temos . Onde é obtido fazendo :
Vamos representar essas forças no desenho (com os valores em ):
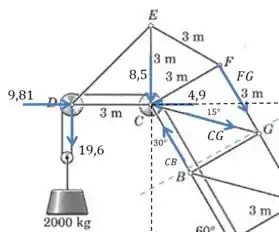
Passo 2
Agora vamos montar equações de equilíbrio, começando com o momento em relação ao ponto :
Nesse caso só ficamos com as forças e a força de :
E agora vamos ver o momento em relação ao ponto . Nesse caso ficamos com as forças , e as de , , e , e então:
É importante olhar para o desenho para encontrar as expressões para as distâncias:
Passo 3
Agora vamos montar a condição de equilíbrio das forças na direção do eixo , com a intenção de encontrar :
Resposta
As forças são (compressão), (tração), (tração).