Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 115
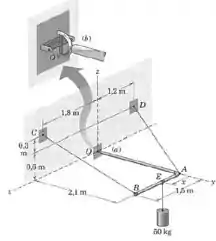
A barra com formato em é sustentada por uma rótula em [caso (a)] e por dois cabos como mostrado. Explique porque essa configuração não está restrita corretamente. (b) A rótula é, agora, substituída pela junta universal, que pode suportar, além das três forças de reação, um momento em relação ao eixo , mas não momentos em relação aos eixos e . Faça um gráfico das forças trativas nos dois cabos, do módulo da força de reação em e do momento de reação em , em função da posição do cilindro de entre . Explique qualquer característica fora do comum nos gráficos. Despreze o peso da barra em todos os casos.
Passo 1
No caso (a) o sistema não está restrito corretamente por uma razão bem direta: os dois cabos e não são paralelos. Como as linhas de ação das trações nesses cabos apontam na direção dos próprios, existe algum ponto, por mais distante que seja, em que essas duas linhas se cruzam.
Se tomarmos esse ponto e ligarmos ele por uma reta até o ponto , teremos definido um eixo em torno do qual as duas trações e as forças em têm momento nulo. Ou seja, nesse caso a barra estará livre para girar em torno dessa linha, puxada pelo peso do cilindro de .
Passo 2
Agora vamos desenhar as forças na situação do caso (mas por conveniência vamos usar a imagem do caso (a)).
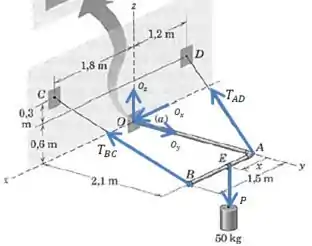
Nosso objetivo é encontrar , , e o momento , que não foi desenhado. Começamos escrevendo as trações e em forma vetorial. Para isso precisaremos dos vetores unitários nas direções e :
E então os dois vetores são:
Passo 3
Agora podemos começar a montar equações de equilíbrio. Vamos primeiro ao equilíbrio das forças em cada direção:
Passo 4
Logo em seguida vamos montar as equações de equilíbrio em relação a cada eixo.
Para o eixo precisamos das componentes em das trações:
Para o eixo precisamos da componente em apenas de e do momento . O momento do peso vai depender do valor de .
E segunido a mesma lógica, para o eixo temos a seguinte equação:
Passo 5
Agora vamos calcular os valores numéricos para poder resolver o sistema:
E esse é um sistema de variáveis desconhecidas e equações (considerando que não é uma variável desconhecida, e sim um valor que varia em um intervalo conhecido).
Lembre-se de que esse é um problema feito para ser resolvido em um computador (até porque seria absurdo resolvê-lo para cada valor no intervalo ).
Mas quando mandamos o computador resolver o sistema para diversos valores de nesse intervalo, vemos que eles são constantes:
E o módulo da força em é:
Substituindo esses valores na terceira equação do sistema, encontramos também a seguinte expressão para o momento :
Resposta
As forças são , e .