Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 97
Calcule o módulo da força suportada pelo pino em no dispositivo em curva, carregado e apoiado como mostrado.
Passo 1
Primeiro precisamos definir um sistema de coordenadas e desenhar as forças que agem sobre o dispositivo.
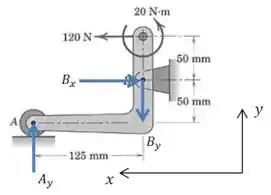
Como sabemos que em só temos uma componente ? Imagine que não existisse um pino em , concorda que o dispotivo tenderia a girar de forma que aquela ponta se movesse na vertical para baixo? A força em é a reação que impede que isso aconteça!
Ok, agora vamos procurar equações de equilíbrio.
Passo 2
Começas com o mais simples: o equilíbrio das forças em cada direção:
Nosso objetivo é calcular o módulo de , ou seja, precisamos das componentes e :
Precisamos descobrir !
Passo 3
Vamos considerar o equilíbrio dos momentos em relação ao ponto :
Apenas a força favorece a rotação no sentido horário, e a força de favorece o sentido anti-horário. Além disso, temos o momento de também nesse sentido.
Para obter o momento temos que multiplicar cada uma das forças pela distância perpendicular até o ponto :
E já que , podemos calcular o módulo de :
Resposta
O módulo da força suportada no pino em é .