Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 163
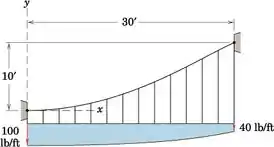
O cabo de massa desprezível é suspenso nos dois pontos fixos mostrados, e a tensão no suporte inferior é suficiente para manter a inclinação zero do cabo naquele ponto. O cabo suporta uma carga unitária w que diminui de 100 lb/pés em x = 0 a 40 lb/pés em x = 30 pés com a diminuição proporcional a x2. Determine a equação da curva assumida pelo cabo.
Passo 1
A primeira coisa que precisamos fazer é determinar os coeficientes da função de carregamento
Função de carga:
Podemos notar que existem dois coeficientes desconhecidos, então precisaremos escrever duas equações para determiná-los
Em x = 0, a intensidade é w = 500, então colocaremos esses valores na função
Em x = 6, a intensidade é w = 900, então colocaremos esses valores na função
Substitua w0 por 500
Passo 2
Como determinamos os coeficientes w0 e k, podemos escrever a função de carregamento como:
Vamos determinar o R resultante integrando a função parabólica ao longo do intervalo:
Substitua x por 30
E a distância do eixo y é
Substitua x por 30
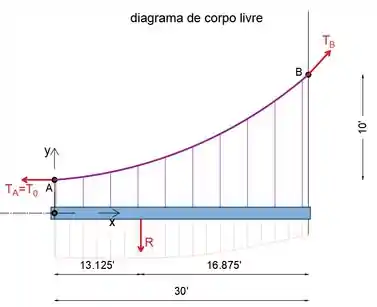
Passo 3
Equacionando a soma dos momentos sobre o ponto B a zero, eliminaremos a tensão no ponto B, de modo que o único desconhecido será T0
Agora que calculamos a tensão T0, usando a expressão (5/13) podemos escrever a função do cabo parabólico como:
Substitua w pela expressão escrita na Etapa 1 e T0 por seu valor.
Integre ambos os lados da equação
Coloque as constantes na frente do sinal integral
Integre o lado direito da equação em relação a dx
Passo 4
Observe que, como a inclinação em , podemos concluir que o coeficiente C1 é igual a zero
Integre novamente os dois lados da equação
Integre o lado direito da equação em relação a dx
Novamente observe que em y = 0 a coordenada y = 0, então podemos concluir que o coeficiente C2 é igual a zero, então a expressão final para a função de cabo parabólico é: