Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 23

O momento de primeira ordem da área sombreada vale Q x .   (a) Determine Q x . (b)Para qual valor de y o Q x é máximo e qual é este valor?

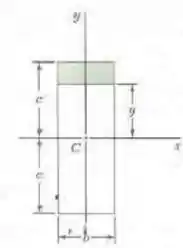
Passo 1

Fala aí galera, vamos pra mais um problema de estática. Sabemos que o momento de primeira ordem da área sombreada será dado pela distância do seu centroide ao centroide da peça multiplicada por sua área. Logo:

A = c - y × b

y - = y + c - y 2

Portanto:

Q x = c - y b + y + c - y 2

Passo 2

Para a letra b, devemos analisar a fórmula:

Q x = c - y b + y + c - y 2 = b + 1 2 c - y b - 1 2  

Podemos ver que Q x é máximo quando y = 0 e vale:

Q x = b + 1 2 c

Resposta

  1. Q x = c - y b + y + c - y 2

  2. y = 0 ; Q x = b + 1 2 c
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O abajur mostrado é construído em aço de 0,6 mm de espessura e é simétrico em relação ao eixo z. Ambas as extremidades superior e inferior estão abertas. Determine a massa do abajur. Considere os raio
O arco circular é girado 360 ° em torno do eixo y. Determine a área da superfície externa S do corpo resultante, que é uma parte de uma casca esférica.
Determine a área da superfície interna (gerada girando ABC completamente em torno do eixo z) do corpo mostrado na seção transversal.
O corpo mostrado em seção transversal é um anel circular completo formado pela rotação da área octogonal em torno do eixo z. Toda a superfície deve ser coberta com um revestimento especial. Determine
Os dois arcos circulares AB e BC são girados em torno do eixo vertical para obter a superfície de revolução mostrada. Calcule a área A do lado de fora dessa superfície.