Calcule a velocidade de impacto de um corpo liberado a partir do repouso a uma altitude . (a) suponha uma aceleração gravitacional constante e (b) considere a variação de com a altitude (veja a seção 1/5). Despreze os efeitos do arrasto atmosférico.
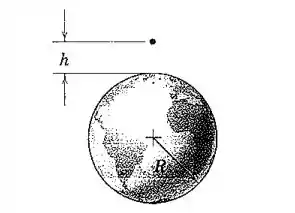
Passo 1
(a) Bom, se a gente supôr que a aceleração é constante a situação fica bastante simples. Vamos ter os seguintes valores:
Perceba que aqui o sentido positivo é vertical para baixo. Como não estamos interessados no tempo, vamos usar a equação de Torricelli:
Passo 2
Beleza, agora vamos parar com as mentiras: vamos levar em conta a variação na aceleração da gravidade. Tudo fica muito mais interessante.
A fórmula para a aceleração da gravidade é:
E nesse caso , já que o corpo cai em linha reta. Além disso, como estamos considerando apenas o efeito da gravidade, temos .
Dessa vez colocamos um sinal negativo porque agora é mais fácil tomar o sentido vertical para cima como positivo.
Vamos usar a definição da aceleração:
E então:
Substituindo a expressão de cima:
Ótimo, podemos resolver essa equação diferencial para encontrar uma relação entre posição e velocidade.
Passo 3
Agora vamos integrar dos dois lados. Lembrando que vai de até (onde é o raio da Terra), enquanto vai de até o valor final que queremos descobrir:
E resolvendo as integrais ficamos com o seguinte:
Substituindo os valores numéricos vamos ficar com o seguinte resultado:
Pronto!
Resposta
(a)
(b)