Uma partícula se move ao longo da direção com aceleração constante. O deslocamento, medido a partir de uma posição apropriada, é de no instante e é zero quando . Se a velocidade da partícula é momentaneamente zero quando determine a aceleração e a velocidade quando

Vamos começar analisando a função da velocidade. Se fizermos um gráfico sabemos que vamos achar uma reta que satisfaça .

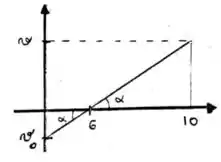
Agora vamos escrever a tangente daquele ângulo :

E igualando as duas expressões:

Mas sabemos que precisa ser um número negativo e que é positivo, então:

Beleza, já temos nosso primeiro resultado.

Outra coisa que podemos extrair do gráfico é a seguinte igualdade:

Vamos pegar a equação da posição:

E substituindo o nossos resultados de cima e também usando :

Além disso, sabemos que

Então:

Pronto, encontramos a velocidade em .

Em seguida queremos encontrar a aceleração:

Pronto!