Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 24

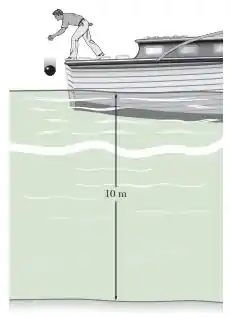
Uma bola de boliche é solta de um barco até que atinja a superfície de um lago com a velocidade de 8   m / s . Considerando que a bola experimenta uma desaceleração de a = 10 - 0,9   v ² quando na água, determine a velocidade da bola quando ela atinge o fundo lago.

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente determine a velocidade da bola quando ela atinge o fundo lago. Vamos trazendo os dados :D

v 0 = 8 m s ,             x - x 0 = 10 m

a = 10 - 0,9 v ² = k   x   ( c 2 - v 2 )

Onde k = 0,9 m - 1     e       c ² = 10 0,9 = 11,111 m ² / s ²

c = 3,3333 m / s

Passo 2

Desde v 0 > c , escreva

a = v d v d x = - k   x   v 2 - c 2 v d v v 2 - c ² = - k d x

Integrando 1 2 I n   x   v 2 - c 2 v 0 v = - k   x   x - x 0 I n v 2 - c 2 v 0 2 - c 2 = - 2 k   x   x - x 0 v 2 - c 2 v 0 2 - c 2 = e - 2 k   x   x - x 0 v 2 = c 2 + v 0 2 - c 2 e - 2 k   x   x - x 0 = 11,111 + 25 2 - 11,111 e - 2 x 0,9 x 30 = 11,111 + 3,89 x 10 - 19 = 11,111   m ² / s ²

Resposta

v = 3,33 m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um irrigador oscilante de jardim, que lança um jato de água com uma velocidade inicial v0 de 8 m/s, é usado para irrigar uma horta. Determine a distância d para o ponto mais afastado B que será irriga
As velocidades dos esquiadores A e B são mostradas na figura. Determine a velocidade de A com relação a B.
Um trabalhador usa água sob alta pressão para limpar o interior de uma longa canalização de drenagem. Se a água é descarregada com uma velocidade inicial v0 de 11,5 m/s, determine (a) a distância d ao
À medida que o bloco deslizante A se movimenta para baixo a uma velocidade de 0,5 m/s, a velocidade em relação a A da porção da correia B entre as polias esticadoras C e D é vCD/A = 2 m/s θ. Determine
Um modelo de foguete é lançado do ponto A com uma velocidade inicial v0 de 75 m/s. Se o paraquedas de descida do foguete não se abre e o foguete cai a 120 m de A, determine (a) o ângulo α que v0 forma