Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 39

Um policial em um carro de patrulha, estacionado em uma zona de 70   k m / h de limite de velocidade, observa um automóvel que passa a uma velocidade lenta e constante. Acreditando que o motorista desse automóvel possa estar embriagado, o policial liga seu carro, acelera uniformemente até 90   k m / h em 8 s e, mantendo uma velocidade constante de 90   k m / h , ultrapassa o motorista 42   s depois desse automóvel ter passado por ele. Sabendo que 18 s se passaram antes do policial começar a perseguir o motorista, determine (a) a distância que o policial percorreu antes de ultrapassar o motorista e (b) a velocidade do motorista.

Passo 1

E aí gurizada tudo belezinha? O enunciado pede que a gente determine a distância que o policial percorreu antes de ultrapassar o motorista e (b) a velocidade do motorista, vejam o esboço abaixo :D

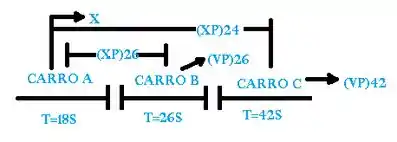
( V P ) 18 = 0 ( V P ) 26 = 90 k m / h = 25 m / s ( V P ) 42 = 90 k m / h = 25 m / s

  1. Carro patrulha:

    2. Para 18 s < t ≤ 26 s : V P = 0 + a P   x   ( t - 18 )

    Em: t = 26 s : 25 m / s = a P   x   26 - 18 s

    Ou a P = 3,125 m / s ²

    Além disso, x P = 0 + 0   x   t - 18 - 1 2 a P   x   ( t - 18 ) ²

    Em t = 26 s : ( x P ) 26 = 1 2   x   ( 3,125 m / s ² )   x   ( 26 - 18 ) ² = 100 m

    Para 26 s < t ≤ 42 s : x P = ( x P ) 26 + ( v P ) 26   x   ( t - 26 )

    Em t = 42 s : ( x P ) 42 = 100 m + ( 25 m / s )   x   42 - 26 s = 500 m

    Passo 2

  2. Para o carro do motorista: x M = 0 + v M t

Em t = 42 s ,     x M = x P : 500 m = v M   x   ( 42 s )

Ou v M = 11,9048 m / s

Resposta

  1. ( x P ) 42 = 0,5 k m
  2. v M = 42,9 k m / h
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O movimento de uma partícula e definido pelas equações x = t2 - 8t + 7 e y = 0,5t2 - 2t - 4, onde x e y são expressos em metros e t em segundos. Determine (a) a intensidade da menor velocidade atingid
Durante a entrega de jornais, uma garota joga um jornal com uma velocidade horizontal v0. Determine o intervalo de valores de v0 para que o jornal caia entre os pontos B e C.
O movimento de uma partícula está definido pelo vetor de posição r = A(cos t + t sen t)i + A(sen t - t cos t)j, onde t e expresso em segundos. Determine os valores de t para os quais o vetor de posiçã
O movimento de uma partícula e definido pelas equações x = t2 - 8t + 7 e y = 0,5t2 - 2t - 4, onde x e y são expressos em metros e t em segundos. Determine (a) a intensidade da menor velocidade atingid
O movimento tridimensional de uma partícula é definido pelo vetor de posição r = (At cos t)i + (A t 2 + 1 )j + (Bt sen t)k, onde r e t estão expressos em metros e segundos, respectivamente. Mostre que