Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 90
Uma calha longa é suportada por uma dobradiça contínua ao longo da aresta inferior e por uma série de cabo horizontais fixados na aresta superior. Determine a tensão em cada um dos cabos no momento que a calha esteja completamente cheia.
Passo 1
Bom galera, a gente vai começar fazendo um diagraminha de corpo livre da pressão da água na calha:
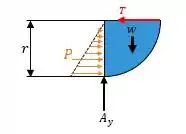
Passo 2
Show de bola, a gente vai pegar um comprimento de de calha pra analisar.
O peso da água na calha pode ser dado por:
E a pressão exercida pela água é encontrada com:
Passo 3
Bom, agora vamos analisar o momento adotando como eixo de rotação e sabendo que a viga está em equilíbrio:
Aplicando os valores fica:
Resposta
Exercícios de Livros Relacionados
O carregamento distribuído atua sobre a viga conforme ilustrado. Determine a intensidade da força resultante equivalente e especifique sua posição, medindo a partir do ponto A .
A viga está sujeita ao carregamento parabólico. Determine um sistema de força e binário equivalente no ponto A.
O túnel submarino no parque aquático é feito de um material de policarbonato transparente, moldado na forma de uma parábola. Determine a intensidade da força hidrostática que atua por metro de comprim
A carga de pressão sobre a placa é exercida pela função p = { - 240 / ( x + 1 ) + 340 }P a . Determine a intensidade da força resultante e as coordenadas dos ponto onde a linha de ação da força interc
A carga sobre a placa varia linearmente ao longo dos lados da placa, de modo que p = 2 3 x 4 - yk P a . Determine a força resultante e sua posição ( x - , y - ) na placa.