Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 119

O túnel submarino no parque aquático é feito de um material de policarbonato transparente, moldado na forma de uma parábola. Determine a intensidade da força hidrostática que atua por metro de comprimento ao longo da superfície A B do túnel. A densidade da água é t w = 1000   k g / m 3 .

Passo 1

O problema quer que a gente encontre a intensidade da força hidrostática por comprimento que atua sobre o túnel.

Primeiro, vamos calcular a força hidrostática resultante que atua sobre o túnel.

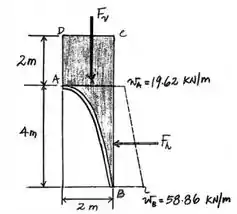
Vamos logo calcular essa área hachurada que representa a água:

A = 2 ⋅ ( 4 + 2 ) - ∫ 0 2 4 - x 2   d x

A = 6,6667

Vamos calcular primeiro a componente em y :

F y = ρ w ⋅ g ⋅ A

F y = 1000 ⋅ 9,81 ⋅ 6,6667 ⋅ 1

F y = 65400   N = 65,4   k N

Passo 2

Agora, vamos analisar calcular a componente em x :

Consideramos a largura do túnel constante em b = 1   m , e a carga horizontal exercida no túnel é distribuída de forma trapezoidal nos pontos A e B , então vamos:

w A = ρ w ⋅ g ⋅ h A ⋅ b

w A = 1000 ⋅ 9,81 ⋅ 2 ⋅ 1

w A = 19,62   k N

E:

w B = ρ w ⋅ g ⋅ h B ⋅ b

w B = 1000 ⋅ 9,81 ⋅ 6 ⋅ 1

w B = 58,86   k N

Então temos:

F x = 1 2 ⋅ w A + w B ⋅ 4

F x = 1 2 ⋅ 19,62 + 58,86 ⋅ 4

F x = 156,96   k N

Passo 3

Por fim, vamos calcular a resultante em módulo das componentes encontradas:

F = F x 2 + F y 2

F = 156,96 2 + 65,4 2

F = 170   k N

Resposta

F = 170   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

117- Quatro vigas, cada qual de comprimento 3 a , são pregadas juntas com um único prego em A , B , C e D . Cada viga é fixada a um suporte localizado a uma distância a a partir da ponta da viga como
118- Quatro vigas, cada qual de comprimento 2 a , são pregadas juntas em seus pontos médios para formar o sistema de suporte mostrado na figura. Considere que apenas forças verticais são exercidas nas
Determine as reações de apoio da viga para a carga dela.
Determine (a) a distância a tal que as reações verticais dos apoios A e B sejam iguais, (b) as reações de apoio correspondentes.
Para a viga e o carregamento mostrados nas figuras, determine (a) a intensidade e a localização da resultante da carga distribuida, (b) as reações de apoio da viga.