Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 71

O caminhão de 5   M g e o carro de 2   M g estão viajando nas velocidades mostradas imediatamente antes de colidirem. Após a colisão o carro move-se com uma velocidade de 15   k m / h para a direita em relação ao caminhão. Determine o coeficiente de restituição entre o caminhão e o carro e a perda de energia devido à colisão.

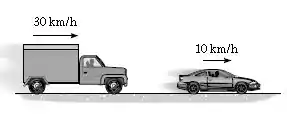
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Primeito vamos transformar estas velocidade para m / s . Temos:

v C a m 1 = 30 10 3 m h 1   h 3600   s

v C a m 1 = 8,333   m / s

v c a r 1 = 16 10 3 m h 1   h 3600   s

v c a r 1 = 2,778   m / s

Agora que sabemos as velocidades antes do impacto, precisamos encontrar as velocidades após o impacto:

→ +       ∑ m v 2 = ∑ m v 3

m C a m v C a m 1 + m c a r v c a r 1 = m C a m v C a m 2 + m c a r v c a r 2

5000 8,333 + 2000 2,778 = 5000 v C a m 2 + 2000 v c a r 2

5 v C a m 2 + 2 v c a r 2 = 47,22

Sabemos que:

v c a r 2 = v C a m 2 + v c a r / c a r 2

Logo:

v c a r 2 = v C a m 2 + [ 15 10 3 m h 1   h 3600   s

v c a r 2 - v C a m 2 = 4,167

Por restituição , temos:

e = v c a r 2 - v C a m 2 v C a m 1 + v c a r 1

e = 4,167 8,333 - 2,778

e = 0,75

Relacionando as equações anteriores, temos:

v c a r 2 = 9,722   m / s

v C a m 2 = 5,556   m / s

A diferença de energia cinética é dada por:

∆ E = T 1 - T 2

T 1 = 1 2 5000 8,333 2 + 1 2 2000 2,778 2

T 1 = 181,33 10 3 J

T 2 = 1 2 5000 5,556 2 + 1 2 2000 9 , 7 22 2

T 2 = 171,68 10 3 J

Resposta

e = 0,75

∆ E = 9,65   k J

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os dois vagões de mina de massas iguais são conectados por uma corda que está inicialmente frouxa. O vagão A recebe um empurrão que transmite a ele uma velocidade de 1,2m / s com o vagão B inicialment
A bola de beisebol está se deslocando com uma velocidade horizontal de 135 k m / h pouco antes do impacto com o bastão. Logo após o impacto, a velocidade da bola de 146g é de 210k m / h direcionada a
O pêndulo balístico é um dispositivo simples para medir a velocidade v de um projétil pela observação do ângulo máximo θ para onde a caixa de areia com o projétil alojado oscila. Calcule o ângulo θ se
O menino de 40k g deu um salto com velocidade a partir da superfície superior e caiu em seu esqueite de 5k g com uma velocidade de 5m / s no plano da figura conforme mostrado. Se o seu impacto com o e
Os terceiro e quarto estágios de um foguete estão se deslocando sem propulsão no espaço com uma velocidade de 18000k m / h quando uma pequena carga explosiva entre os estágios os separa. Imediatamente