Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 214

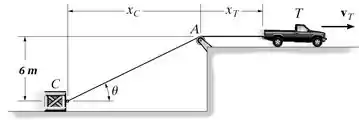
Se o caminhão se desloca a uma velocidade de escalar constante vT = 1,8 m/s, determine a velocidade escalar da caixa para qualquer ângulo θ da corda. A corda tem um comprimento de 30 m e passa sobre uma polia de tamanho desprezível em A. Dica: Relacione as coordenadas xT e xC ao comprimento da corda e calcule a derivada temporal. Em seguida, substitua a relação trigonométrica entre xC e θ.

Passo 1

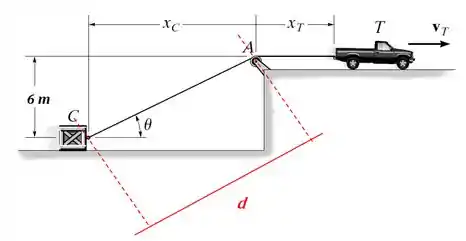
Primeiramente deve-se relacionar as coordenadas xT e xC ao comprimento da corda, conforme sugerido no problema. Para tanto , se estabelece a seguinte relação pitagórica:

d = 6 2 + x C 2

Assim, o comprimento total da corda será dado por :

30 = x T +   d = x T + 6 2 + x C 2 (1)

Passo 2

Após determinar a função que realiona os deslocamentos xT e xC exposto em (1), deve-se fazer a sua derivada temporal, de forma agora a relacionar as velocidades do veículo e da caixa. Sabendo que x T ˙ = vT = 1,8 m/s e que x C ˙ = vC.

1 2 6 2 + x c 2 - 1 2 2 x c x c ˙ +   x T ˙ = 0

1 2 6 2 + x c 2 - 1 2 2 x c v c +   1,8 = 0 (2)

Passo 3

Agora , deve-se , substituir a relação trigonométrica entre xC e θ , x c = 6 cot ⁡ θ , em (2). De forma que :

1 2 6 2 + ( 6 cot ⁡ θ ) 2 - 1 2 2 * 6 cot ⁡ θ v c +   1,8 = 0

( 6 cot ⁡ θ ) v c 36 +   36  cot 2 ⁡ θ =   - 1,8

( 6 cot ⁡ θ ) v c 36 1 +    cot 2 ⁡ θ =   - 1,8

( 6 cot ⁡ θ ) v c 6 1 +    cot 2 ⁡ θ =   - 1,8

Sabendo que 1 +    cot 2 ⁡ θ =   csc 2 ⁡ θ , temos que:

( cot ⁡ θ ) v c csc 2 ⁡ θ =   - 1,8

( cot ⁡ θ ) v c csc ⁡ θ =   - 1,8

E sabendo que cot ⁡ θ csc ⁡ θ =   cos ⁡ θ , temos que :

v c cos ⁡ θ =   - 1,8

Resposta

Com base nos passos 1, 2 e 3 foi possível determinar que para qualquer ângulo θ a velocidade escalar da caixa será dada pela função abaixo.

v c =   - 1,8 cos ⁡ θ   m / s

Ou ainda

v c =   - 1,8   sec ⁡ θ = 1,8 sec ⁡ θ   m / s →  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois ciclistas A e B movem-se com a mesma velocidade escalar constante de v. Determine a velocidade de A em relação a B se A se desloca ao longo da pista circular. Enquanto B se desloca ao longo do di
No instante mostrado, o carro A está se deslocando com uma velocidade de 30 m/s e tem uma aceleração de 2 m/s2 ao longo da autoestrada. No mesmo instante, B está se deslocando na curva do trevo rodovi
O movimento do anel em A é controlado por um motor em B de tal maneira que quando o anel está em s A = 3 m ele está se desacelerando a razão de 1 m/ s 2 . Determine a velocidade e aceleração de um pon
O motor em C puxa o cabo com uma aceleração de a c = ( 3 t 2 ) m/s2, onde t é dado em segundos. O motor em D puxa o cabo a a d = 5 m/ s 2 . Se ambos motores partem ao mesmo tempo do repouso quando d=3
Se os motores em A e B recolhem seus cabos conectados com uma aceleração a=0,2t m/s2, onde t é dado em segundos, determine a velocidade escalar do bloco quando ele alcança uma altura de h=4m, partindo