Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 211

O movimento do anel em A é controlado por um motor em B de tal maneira que quando o anel está em s A = 3 m ele está se desacelerando a razão de 1  m/ s 2 . Determine a velocidade e aceleração de um ponto sobre o cabo no instante quando ele é puxado na direção do motor B

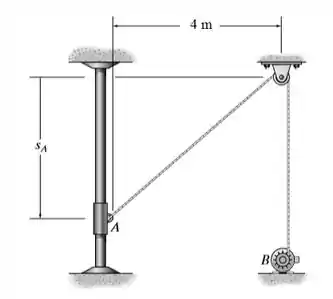
Passo 1

Analisando as cordas, temos que

s A 2 + 4 2 + s B = l

Derivando duas vezes a equação para encontrar a velocidade e aceleração

1 2 ( s A 2 + 16 ) - 1 2 ( 2 s A ) v A + v B = 0

Então v B será

v B = - 2 s A v A ( s A 2 + 16 ) - 1 2

Derivando , iremos encontrar a aceleração em B, então

a B = - [ ( v A ) 2 ( s A 2 + 16 ) - 1 / 2 + s A a A ( s A 2 + 16 ) - 1 / 2 + s A v A ( - 1 2 ) ( s A 2 + 16 ) - 3 / 2 ( 2 s A v A )

Substituindo valores, temos que

v B = 1,20 m/s

a B = 1,11  m/ s 2

Resposta

A velocidade e a aceleração em B serão, respectivamente:

v B = 1,20 m/s

a B = 1,11  m/ s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pequeno avião A inicialmente voando para o norte com uma velocidade em relação ao solo de 225k m / h encontra um vento oeste de 75k m / h (soprando para o leste). O avião B voando para o oeste com u
Uma mulher P caminha em uma rua de leste para oeste a uma velocidade de 6k m / h . O vento sopra do noroeste como mostrado a uma velocidade de 4k m / h . Determine a velocidade do vento em relação à m
O carrinho de mineração C é puxado pelo motor M através de um conjunto de cordas e polias. Determinar a velocidade do ponto P de tal maneira que a velocidade escalar de C seja v c = 2 m / s .
O caminhão em C puxa o cabo 1,2 m para a direita, determinar o deslocamento do tronco em B.
Determinar a velocidade escalar que o bloco B quando A se move para baixo com uma velocidade escalar va=4m/s.