Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 229

Dois ciclistas A e B movem-se com a mesma velocidade escalar constante de v. Determine a velocidade de A em relação a B se A se desloca ao longo da pista circular. Enquanto B se desloca ao longo do diâmetro do círculo.

Passo 1

Pela figura dada pela questão é possível concluir a seguinte direção para a velocidade do ciclista A

V A =   V A sin ⁡ θ i +   V A c o s ⁡ ( θ ) j

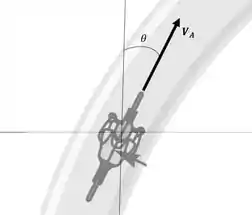
E a para velocidade do ciclista B que está em trajetória retilínea,

V B =   V B   i

Passo 2

Para determinar a velocidade B em relação a A é necessário aplicar a seguinte equação,

V B =   V A +   V B / A

V B / A =     V A -   V B  

V B / A =   V A sin ⁡ θ i +   V A cos ⁡ θ j -   V B   i  

Como V A = V B = v  

V B / A = ( v sin ⁡ θ -   v ) i   +   v cos ⁡ θ j  

Passo 3

o modulo da velocidade V B / A ,

V B / A =   ( v sin ⁡ θ -   v ) 2 + v cos ⁡ θ 2

V B / A =   2 v 2 - 2 v 2 sin ⁡ θ

V B / A =   v 2 ( 1 - sin ⁡ θ )

Resposta

velocidade relativa é

V B / A = ( v sin ⁡ θ -   v ) i   +   v cos ⁡ θ j  

E seu modulo

V B / A =   v 2 ( 1 - sin ⁡ θ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Após partir da posição marcada com um “ x ”, um jogador de futebol americano B corre modificando a trajetória no padrão apresentado, fazendo um corte em P e depois correndo com uma velocidade constant
A aeronave A com equipamento de detecção por radar está voando horizontalmente a uma altitude de 12k m e está aumentando sua velocidade na taxa de 1,2m / s cada segundo. Seu radar capta uma aeronave B
Um veleiro deslocando-se na direção mostrada está navegando a barlavento contra um vento norte. O instrumento que mede a velocidade do barco registra uma velocidade do casco de 6,5 nós. Uma corda leve
O trem A viaja com uma velocidade constante v A = 120k m / h ao longo da estrada de ferro reta e horizontal. O motorista do carro B , antecipando a passagem de nível ferroviária C , diminui a velocida
O jogador de hóquei A conduz o disco com seu taco e se desloca na direção mostrada com uma velocidade v A = 4m / s . Na passagem do disco para seu companheiro de equipe parado B , qual ângulo α a dire