Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 228

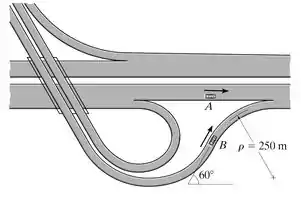
No instante mostrado, o carro A está se deslocando com uma velocidade de 30 m/s e tem uma aceleração de 2 m/s2 ao longo da autoestrada. No mesmo instante, B está se deslocando na curva do trevo rodoviário com uma velocidade escalar de 15 m/s, a qual está reduzindo na razão de 0,8   m/s2. Determine a velocidade relativa e aceleração relativa de B em relação a A neste instante.

Passo 1

Os carros A e B se movimentando podem ser tratados como partículas para esse caso. Então, para se determinar a velocidade e aceleração de B em relação a A é necessário aplicar as equações que relacionam as velocidades e acelerações absolutas e relativas das partículas.

V B =   V A +   V B / A

a B =   a A +   a B / A

Passo 2

Para determinar a velocidade B em relação a A é necessário aplicar a seguinte equação,

V B =   V A +   V B / A

15 sin ⁡ 60 ° j + 15 cos ⁡ 30 ° i = 30 i +   V B / A    

V B / A = - 22,5 i + 12,99 j   m / s

o modulo da velocidade e a direção V B / A ,

V B / A =   - 22,5 2 + 12,99 2 = 26   m / s

θ =   tan - 1 ⁡ - 12,99 22,5 = 150 °

Passo 3

Para determinar a aceleração de B em relação A , primeriramente deve se notar que o carro B tem uma trajetória curva, então possui uma aceleração normal e tangente. Conforme o carro B descrever a trajetória curva em “desaceleração” , vetores de aceleração tangente e normal possuiem as seguintes orientações.

a B =   a B t +   a B n  

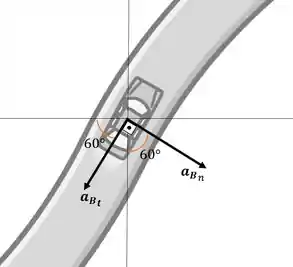
O modulo da aceleração normal pode ser calculado por

a B n = V B 2 ρ = 15 2 250 = 0,9   m / s 2

De acordo com direções, os vetores de aceleração normal e tangente do carro B, podem ser escritos sendo,

a B t = - 0,8 cos ⁡ 60 ° i - 0,8 sin ⁡ 60 ° j  

a B n = 0,9 sin ⁡ 60 ° i - 0,9 cos ⁡ 60 ° j

Passo 4

Para determinar a aceleração B em relação a A é necessário aplicar a seguinte equação, e carro A está com velocidade constante, portanto a aceleração é zero.

a B =   a A +   a B / A

- 0,8 cos ⁡ 60 ° + 0,9 sin ⁡ 60 ° i + - 0,8 sin ⁡ 60 ° - 0,9 cos ⁡ 60 ° j = 2 i + a B / A

a B / A = - 1,6206 i - 1,1428   j   m / s 2

o modulo da aceleração e a direção a B / A ,

a B / A =   1,6206 2 + 1,1428 2 = 1,98   m / s 2

ϕ =   tan - 1 ⁡ 1,6206 1,1428 = 215,2 °

Resposta

A velocidade relativa é

V B / A = - 22,5 i + 12,99 j   m / s

Sendo o modulo de 26 m/s e a direção de 150 °  

A aceleração relativa é

a B / A = - 1,6206 i - 1,1428   j   m / s 2

Sendo o modulo de 1,98 m/s2 e a direção de 215,2 °  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os trens A e B circulam sobre vias paralelas. O trem A tem uma velocidade de 80k m / h e está diminuindo na taxa de 2m / s 2 , enquanto o trem B tem uma velocidade constante de 40k m / h . Determine a
O jato de transporte B está voando para o norte com uma velocidade v B = 600k m / h quando uma aeronave menor A passa por baixo do transporte dirigida na direção 60 ° mostrada. Para os passageiros em
O carro A tem uma velocidade para a frente de 18k m / h e está acelerando a 3m / s 2 . Determine a velocidade e a aceleração do carro em relação ao observador B , que é levado em uma cadeira sem rotaç
Para o instante representado, o carro A tem uma aceleração na direção do seu movimento, e o carro B tem uma velocidade de 72k m / h que está aumentando. Se a aceleração de B como observada a partir de
Para o instante representado, o carro A tem uma velocidade de 100k m / h , que está aumentando na taxa de 8k m / h cada segundo. Simultaneamente, o carro B também tem uma velocidade de 100k m / h enqu