Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 107

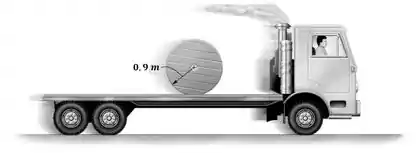
O caminhão transporta a bobina que tem uma massa de 100 kg e um raio de giraçao K G = 0,6 m. determine a aceleração angular da bobina se ela não estiver amarrada ao caminhão e ele começa a acelerar a 1,5 m/s2 . Os coeficientes de atrito cinético e estático entre a bobina e o piso da carroceria do caminhão são μ k = 0,15 e μ s = 0,1 , respectivamente.

Passo 1

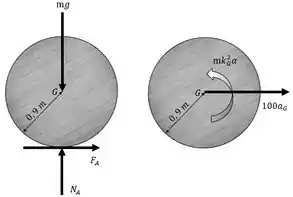
O diagrama de corpo livre e cinemático são mostrados na figura abaixo:

Passo 2

Tendo as informações do DCL e do DC, é possível aplicar 2º lei de Newton para a análise do corpo

↑ ∑ F y = m a G y

N - 100 ( 9,81 ) = 0

N = 981   N

→ ∑ F x = m a G x

F = 100 a G

↻ ∑ M G = I G α

F 0,9 = 100 0,6 2 α

Passo 3

Suponha que não ocorra escorregamento no ponto de contato. Consequentemente,

a A t = 1,5   m / s 2

Como as incógnitas são F ,   a G e α é necessária uma quarta equação podendo ser a equação de aceleração relativa.

a A = a G + a A / G t + a A / G n

a A t + a A n = a G + 0,9 α + a A / G n

→   1,5 = a G + 0,9 α    

Resolvendo o sistema,

F = 100 a G F 0,9 = 100 0,6 2 α 1,5 = a G + 0,9 α

a G = 0,46   m / s 2

F = 46,15   N

α = 1,15   r a d / s 2

Desde de

F A m a x = μ k 100 = 0,15 981 = 147,15   N > 46,15   N , dessa forma há deslizamento.

Resposta

A aceleração angular da bobina é 1,15   r a d / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A barra fina uniforme de 60 kg está inicialmente em repouso sobre um plano horizontal liso quando as forças são aplicadas. Determine a aceleração do centro de massa da barra e a aceleração angular da
A barra fina de 12 kg está presa com pino ao rolete pequeno A que desliza livremente ao longo da ranhura. Se a barra é solta do repouso em θ = 0 ° , determine a aceleração angular da barra e a acelera
A esfera de 20 kg rola para baixo sobre o plano inclinado sem deslizar. Determine a aceleração angular da esfera e a aceleração de seu centro de massa.
A roda de 20 kg tem um raio de giração em relação a seu centro O de k O = 300m m . Quando a roda é submetida ao momento de binário, ela desliza na medida em que rola. Determine a aceleração angular da
Dois homens exercem forças verticais constantes de 200 N e 150 N nas extremidades A e B de um pranchão uniforme que tem uma massa de 25 kg. Se o pranchão está originalmente em repouso na posição horiz