Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 16
A esfera de 20 kg rola para baixo sobre o plano inclinado sem deslizar. Determine a aceleração angular da esfera e a aceleração de seu centro de massa.
Passo 1
Começaremos o exercício aplicando o somatório de momentos com relação ao ponto de apoio da esfera no chão conforme diagrama a seguir:
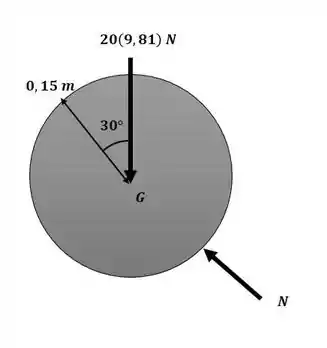
Essa será nossa equação 1.
Passo 2
Como no enunciado foi dito que a esfera não desliza, podemos escrever sua aceleração de centro de massa da seguinte forma:
Passo 3
Agora iremos substituir a expressão obtida no passo 2 na equação do passo 1:
E substituindo esse valor na expressão do passo 2:
Resposta
Exercícios de Livros Relacionados
Um motor fornece um torque constante M = 2 N.m para o eixo de 50 mm de diâmetro O conectado ao centro do volante de 30 kg. O atrito resultante do mancal F, que o mancal exerce sobre o eixo, atua tange
O diagrama cinético representando o movimento rotacional geral de um corpo rígido em torno de um eixo fixo passando por O é mostrado na figura. Mostre que I G α pode ser eliminado deslocando os vetore
A barra fina de 4 kg é suportada horizontalmente por uma mola em A e uma corda em B. Determine a aceleração angular da barra e a aceleração do centro de massa da barra no instante que a corda em B é c
A bobina uniforme está apoiada em dois roletes em A e B. Determine a força constante P que tem de ser aplicada ao cabo a fim de desenrolar 8 m de cabo em 4 s partindo do repouso. Também calcule as for
A pá única PB do ventilador tem uma massa de 2 kg e um momento de inércia I G = 0,18 kg.m² em relação a um eixo passando pelo seu centro de massa G. Se a pá é submetida a uma aceleração angular α = 5