Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 18
A barra fina de 12 kg está presa com pino ao rolete pequeno A que desliza livremente ao longo da ranhura. Se a barra é solta do repouso em , determine a aceleração angular da barra e a aceleração do rolete imediatamente após ela ser solta.
Passo 1
Começaremos o exercício aplicando as equações do movimento para o sistema de acordo com o diagrama a seguir:
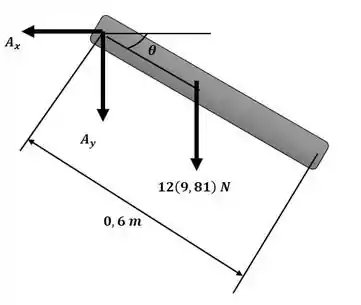
Essa será nossa equação número 1.
Passo 2
Agora iremos aplicar a equação da aceleração vista no capítulo 16, e sabendo que :
Igualando as componentes, temos:
Essa será nossa equação número 2.
Passo 3
Agora iremos substituir a equação 2 na equação 1:
Agora substituindo esse valor na equação 2:
Resposta
Exercícios de Livros Relacionados
Se o motor no Problema 17.60 é desengatado do eixo assim que o volante está girando a 15 rad/s, de maneira que M = 0, determine quanto tempo vai levar antes que a resultante da força de atrito do manc
Um cabo é desenrolado de uma bobina apoiada em pequenos roletes em A e B exercendo uma força T = 300 N no cabo na direção mostrada. Calcule o tempo necessário para desenrolar da bobina 5 m de cabo se
O pêndulo consiste de uma esfera de 15 kg e uma barra fina de 5 kg. Calcule a reação no pino O logo após a corda AB ser cortada.
Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considera
Os passageiros, a gôndola e sua estrutura de balanço têm uma massa total 50 Mg, um centro de massa em G e um raio de giração k B = 3,5 m. Adicionalmente, o bloco de aço de 3 Mg em A pode ser considera