Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 99
Dois homens exercem forças verticais constantes de 200 N e 150 N nas extremidades A e B de um pranchão uniforme que tem uma massa de 25 kg. Se o pranchão está originalmente em repouso na posição horizontal, determine a aceleração inicial de seu centro e sua aceleração angular. Suponha que o pranchão é uma barra fina.
Passo 1
Começaremos o exercício calculando o momento de inércia do pranchão em relação ao seu centro de massa:
Passo 2
Agora iremos aplicar as equações de equilíbrio para o sistema ilustrado na figura a seguir:
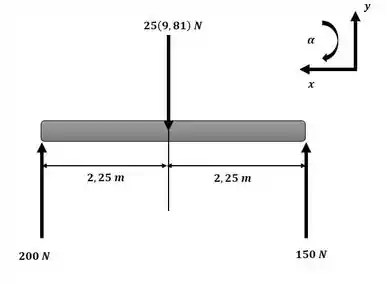
Passo 3
Agora iremos aplicar o somatório de momento em relação ao centro de massa do pranchão:
Resposta
Exercícios de Livros Relacionados
A barra uniforme de 50 kg está em repouso em uma posição vertical quando a corda fixada a ela em B é submetida a uma força P = 250 N. Determine a aceleração angular inicial da barra e a intensidade da
Inicialmente, a roda A gira no sentido horário com uma velocidade anular constante de ω = 100 rad/s. Se A é colocada em contato com B, que é mantida fixa, determine o número de revoluções antes que a
A barra fina uniforme tem uma massa de 9 kg. Se a mola está distendida quando θ = 0°, determine a intensidade da força reativa exercida sobre a barra pelo pino A quando θ = 45°, se, nesse instante, ω
O disco tem uma massa de 20 kg e está originalmente girando na extremidade da escora com uma velocidade angular ω = 60 rad/s. Se ele é, então, colocado contra a parede, onde o coeficiente de atrito ci
A barra tem uma massa m e um comprimento l. Se ela é solta do repouso da posição θ = 30°, determine sua aceleração angular e as componentes verticais e horizontais da reação no pino O.