Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.3 - Ex. 32
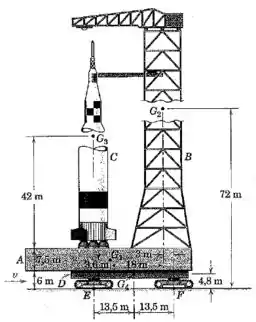
A figura mostra a plataforma móvel de lançamento do foguete saturno V juntamente com a torre umbilical , o foguete sem combustível , e o veículo de transporte sobre esteiras , que carrega o sistema para o local do lançamento. As dimensões aproximadas da estrutura e as localizações do centro de massa são fornecidas. As masssas aproximadas são , , , e . A distância mínima de parada a partir da velocidade máxima de é de . Calcule a componente vertical da reação sob a unidade de esteiras dianteira durante o período de desaceleração máxima.
Passo 1
Primeiro vamos calcular a aceleração do sistema, considerando que ele vai de para o repouso ao longo de uma distância de .
Se a aceleração é constante, podemos dizer que:
Passo 2
Agora vamos fazer um esquema da situação.
Começamos calculando os momentos resultantes atuando no centro de massa de cada corpo:
Para deixar o desenho mais claro começamos apenas com as forças horizontais:
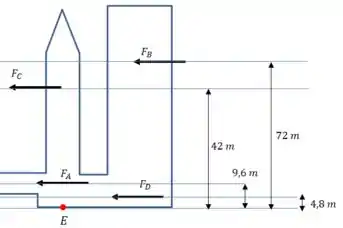
E vamos escrever os momentos dessas forças:
E vamos substituir agora com , deixando as massas em toneladas:
Passo 3
Ok, esse é o torque resultante. Isso quer dizer que a soma dos torques das forças que agem sobre o sistema tem que ser igual a isso.
Essas forças são os pesos de cada parte, e as normais e . Entretanto, quando escolhemos como nosso ponto de referência, o peso da parte e a normal têm torque nulo:
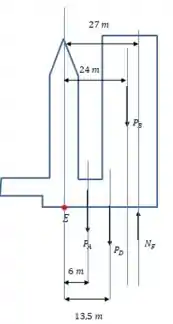
E a soma desses torques é:
E igualando isso ao resultado anterior:
Resposta
A componente vertical da reação é .