Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 199
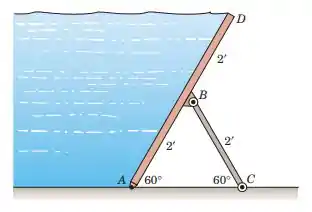
Um canal de água doce com 10 pés de largura (normal para o plano do papel) é bloqueado em sua extremidade por uma barreira retangular, mostrada na seção ABD. As escoras de suporte BC são espaçadas a cada 2 pés ao longo de 10 pés largura. Determine a compressão C em cada biela.Negligencie os pesos dos membros.
Passo 1
E ai gurizada tudo belezinha???
Note que para determinar a pressão da lata C na escora, teremos que calcular o desempenho na parede a partir da água.
Observe também que a água está sempre agindo normalmente em relação à parede da água.
Uma vez que o peso específico da água doce é:
, podemos escrever a expressão acima como:
No esboço abaixo, podemos ver que o ponto A está em profundidade de:
Portanto, a pressão atuando no ponto A é:
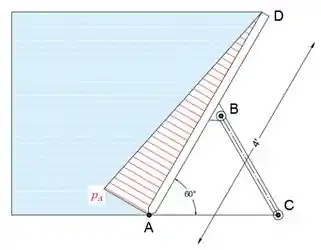
Observe que este é um problema tridimensional, que podemos resolver como bidimensional convertendo a pressão que atua na parede para atuar em uma linha. Uma vez que a parede é suportada por escoras a cada 2 pés, isso significa que cada escora suporta a parte de 2 pés de comprimento do canal de água (não importa se o canal tem 10 pés ou 1000 pés de largura, cada strut suporta a largura de 2 pés ), portanto, a pressão da largura de 2 pés atingindo em uma linha é:
Passo 2
A seguir, isolaremos e desenharemos o diagrama de corpo livre da parede.
Observe que a escora BC é um membro de duas forças, o que significa que a linha de ação da força de compressão C passa pelas juntas B e C.
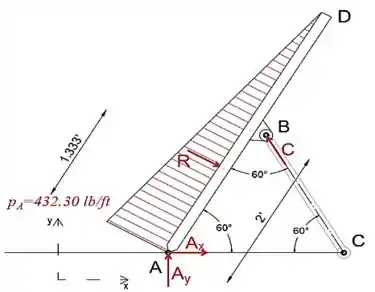
Substituímos a carga distribuída por sua resultante que atua no centro do triângulo
Passo 3
Ao igualar a soma dos momentos sobre o ponto A a zero, eliminaremos as forças de reação em A, de modo que a única incógnita será a força C.
A partir daqui, podemos expressar a força C como:
Substitua R por seu valor.
Calculando a expressão acima, obtivemos que a força C na biela é: