Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 57
5.57. Determine the distance from the bottom of the base plate to the centroid of the built-up structural section shown.
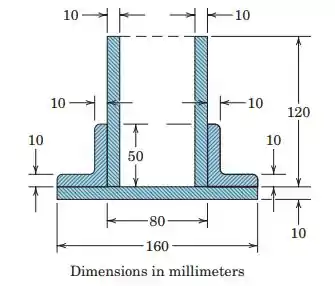
Passo 1
Vamos em busca de mais um centroide!
Essa figura é um pouco complicada para calcular o centroide, por isso vamos separar em várias figuras mais fáceis de calcular:
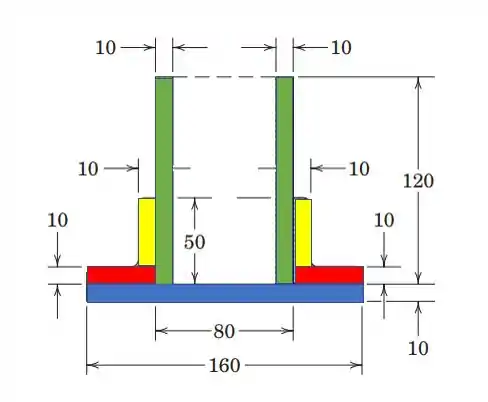
Então temos sete figuras agora, todas são retângulos, mas para nossa felicidade tem muita simetria aqui, olha só, os retângulos de cores iguais têm mesma área e mesma coordenada de centroide.
Passo 2
Podemos começar com o retângulo mais abaixo, de cor azul. Vamos começar pela área:
E sua coordenada é:
Passo 3
Agora vamos nos focar nos retângulos vermelhos. Começando pela área, talvez seja um pouco complicado ver o tamanho da base desse retângulo, mas podemos ver pela figura que a base é:
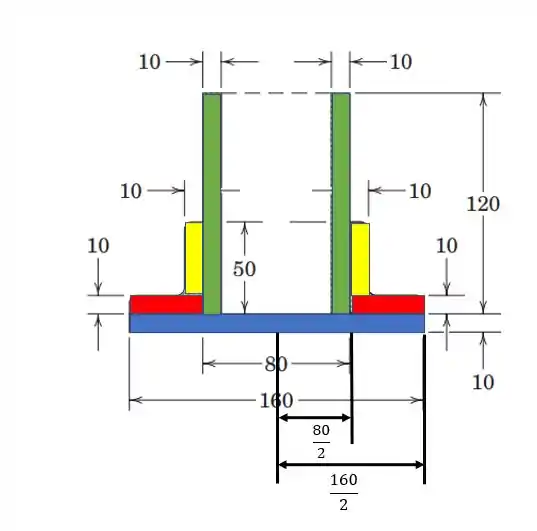
Então a área é
Agora vamos para a coordenada do centroide, mas para isso vamos mudar o centro do sistema de coordenadas primeiro.
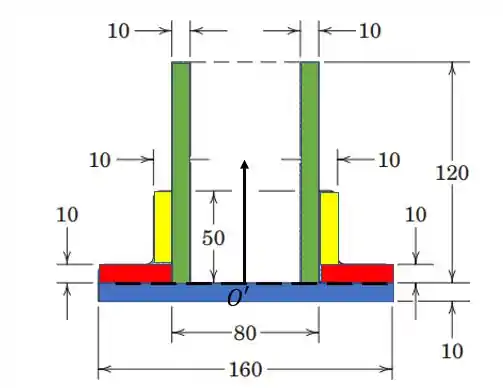
A coordenada de é .
Agora usando o sistema original de coordenadas:
Então
Passo 4
Agora vamos para os retângulos amarelos. Começando pela área
Para calcular a coordenada do centroide vamos subir um pouco mais a origem .
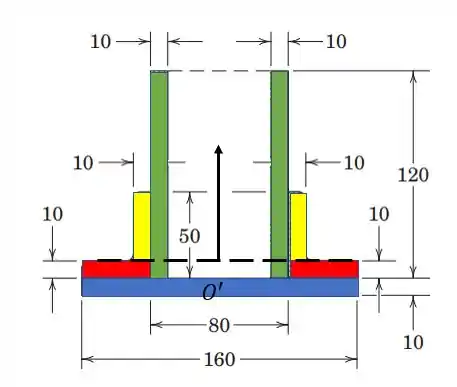
Agora está em .
A coordenada do centroide é:
No sistema de coordenadas original:
Passo 5
Só faltam os retângulos verdes agora.
Agora vamos descer , e voltar para .
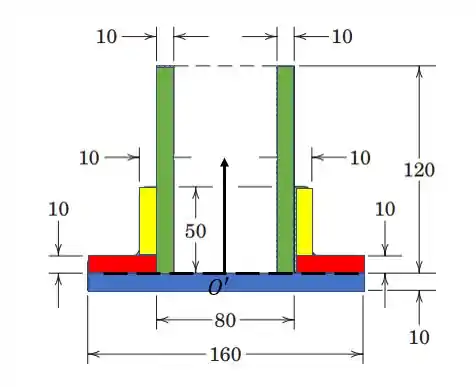
Vamos lá:
Então
Passo 6
Agora vamos calcular o centroide da figura completa:
Isso fica
Agora vamos substituir esses valores
Fazendo essa conta toda aqui ficamos com