Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 15.Problemas - Ex. 50
O canhão de mola de repousa sobre a superfície lisa. Ele dispara uma bala de massa , a uma velocidade relativa ao canhão, na direção mostrada. Se o canhão está originalmente em repouso, determine a distância horizontal , que a bala estará da posição inicial do canhão, no instante em que atingir sua maior altura em . Despreze a dimensão do canhão.
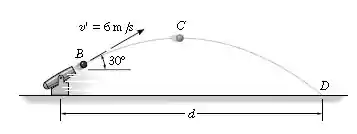
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Aplicando conservação de quantidade de movimento, temos:
Substituindo os valores, temos:
Analisando o movimento relativo, temos:
Logo:
O tempo de voo é dado por:
A altura máxima é de:
A distância do movimento da bala é:
A distância percorrida pelo canhão é:
A distância entre o canhão e a bala é:
A magnitude da distância é:
Resposta
Exercícios de Livros Relacionados
Para a partícula do Problema 12.74, determine o componente tangencial Ft da força central F ao longo da tangente ao caminho da partícula para (a) θ = 0, (b) θ - 45 °.
Uma partícula de massa m é projetada do ponto A com uma velocidade inicial v0 perpendicular à linha OA e se move sob uma força central F direcionada para longe do centro de força O. Sabendo que a part
Mostre que o raio r da órbita de uma lua de um determinado planeta pode ser determinado a partir dos raios R do planeta, da aceleração da gravidade na superfície do planeta e do tempo necessário para
Para a partícula do Problema 12.76 mostre (a) que a velocidade da partícula e a força central F são proporcionais à distância r da partícula ao centro de força O, (b) que o raio de curvatura do caminh
Uma espaçonave é colocada em uma órbita polar em torno do planeta Marte a uma altitude de 380 km. Sabendo que a densidade média de Marte é 3,94 Mg / m³ e que o raio de Marte é 3397 Km, determine (a) o