Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.10 - Ex. 232
Um projetista inexperiente de um leito de estrada para um novo trem de alta velocidade propôs unir uma seção reta da ferrovia a uma seção circular de de raio como apresentado. Para um trem que viajaria a uma velocidade constante de , represente graficamente o módulo de sua aceleração em função da distância ao longo da ferrovia entre os pontos e e explique porque este projeto é inaceitável.
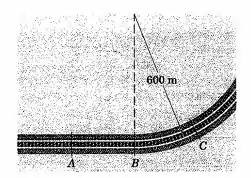
Passo 1
A aceleração do trem tem duas componentes: uma tangencial e uma normal (centrípeta).
A aceleração tangencial muda apenas o módulo da aceleração , e a aceleração normal muda apenas a direção.
Como o módulo da velocidade do trem é sempre constante:
E tirando o módulo:
Passo 2
Nosso objetivo agora é escrever esse módulo da aceleração em função da distância percorrida entre os pontos e :
Como entre e o movimento é retilíneo, não existe aceleração centrípeta, ou seja:
E depois que o trem entra na trajetória circular a aceleração centrípeta passa a ser constante e igual a:
Ou seja:
Representando isso graficamente:
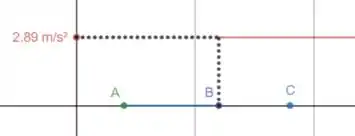
Apesar de possível, o gráfico deixa bem claro porque esse projeto é “inaceitáel”. Os passageiros dentro do trem experimentariam essa aceleração abrupta como forças de inércia bastante fortes e desconfortáveis.
Resposta
O projeto geraria uma mudança muito forte e repentina na aceleração do trem, gerando risco aos passageiros.