Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 88
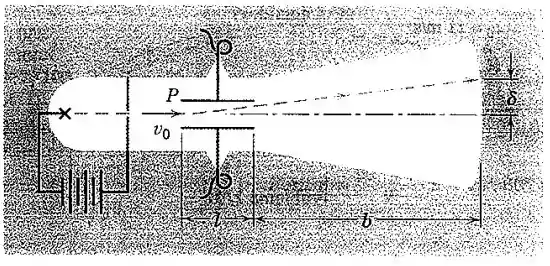
No tubo de raios catódicos, os elétrons viajando horizontalmente a partir de sua fonte com a velocidade são definidos por um campo elétrico devido ao gradiente de tensão entre as placas . A força de deflexão provoca uma aceleração na direção vertical no desenho igual a , onde é a carga do elétron e é a sua massa. Quando ultrapassam as placas, os elétrons viajam em linha reta. Determine a expressão para a deflexão para as dimensões indicadas para o tubo e para a placa.
Passo 1
Pessoal, pra gente determinar a expressão de , precisamos calcular com qual velocidade vertical o elétron deixa a placa. Mas primeiro, do movimento horizontal (velocidade constante) obtemos a seguinte equação:
onde é o tempo até o elétron sair da placa.
Para o movimento vertical dentro da placa, temos o seguinte:
Quando tivermos , ou seja, quando o elétron sair da placa, a velocidade será . Aí substituímos isso na equação:
Passo 2
Show! Agora que a gente sabe a velocidade de saída da placa , podemos calcular a altura do elétron imediatamente após a saída da placa. Faremos isso por meio da seguinte fórmula:
Além disso, como o elétron passa a viajar em linha reta após a saída da placa, é interessante calcular a inclinação dessa reta. Considere o ângulo que a velocidade de saída faz com a horizontal, então será essa inclinação:
Passo 3
Agora considere o triângulo retângulo cujos catetos têm medidas e . A hipotenusa desse triângulo faz com a horizontal um ângulo igual a . Olha só:
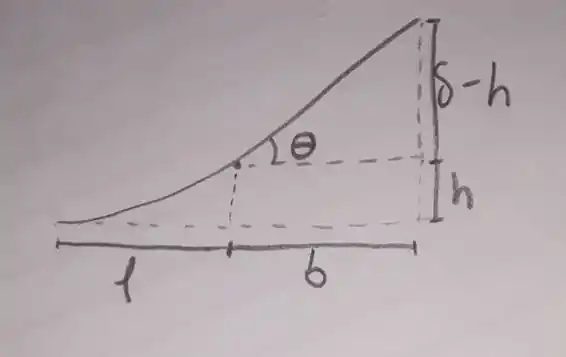
Então podemos escrever:
Beleza! Agora é só substituir os valores de e já encontrados: