Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 184

Considerando que o momento mostrado é substituído por uma força vertical de 10 kN aplicada no ponto D e no sentido descendente, determinar a tensão (a) ponto A; (b) ponto B

Passo 1

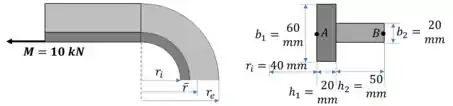
Para resolver a questão, precisamos calcular o raio do centroide e o raio da linha neutra da seção, que são dados por:

r - = A 1 r 1 - + A 2 r 2 - A 1 + A 2

R = A 1 + A 2 b 1 ln ⁡ r e r i 1 + b 2 ln ⁡ r e r i 2

Vamos fazer uma tabela com as principais propriedades da seção transversal

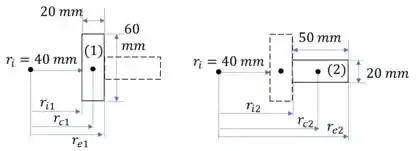
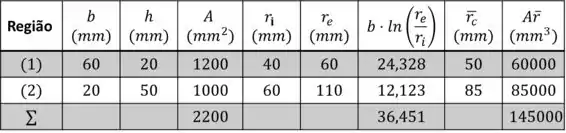
r - = A 1 r 1 - + A 2 r 2 - A 1 + A 2 = 145000 2200 = 65,909   m m R = A 1 + A 2 b 1 ln ⁡ r e r i 1 + b 2 ln ⁡ r e r i 2 = 2200 36,451 = 60,356   m m e = r - - R = 5,5535   m m

Passo 2

A força atuando sobre o ponto D vai gerar uma reação no apoio F que é igual a carga aplicada, e um momento M . As reações atuam em cima do centroide!

M = F ⋅ ( 100   m m + r - ) = 10   k N ⋅ 165,909   m m = 1,66 ⋅ 10 6   N ⋅ m m

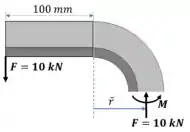
Passo 3

Show!

Agora é só calcular as tensões em cada ponto. CUIDADO! Não esqueça de considerar a tensão de compressão gerada pela força F

σ A = - P A + M r i - R A e r 1

σ A = - 10   k N 2200   m m 2 + 1,66 ⋅ 10 6   N m m ⋅ 40   m m - 65,909   m m 2200   m m 2 ⋅ 5,5535   m m ⋅ 40   m m

σ A = - 73,65   M P a

A tensão no ponto B é uma tração:

σ B = M r e - R A e r e

σ B = - 10   k N 2200   m m 2 + 1,66 ⋅ 10 6   N m m ⋅ 110   m m - 65,909   m m 2200   m m 2 ⋅ 5,5535   m m ⋅ 110   m m

σ B = 56,74   M P a

Resposta

  1. σ A = - 73,65   M P a
  2. σ B = 56,74   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qualquer dar três cargas axiais, de intensidade P = 45 kN podem ser aplicadas na extremidade de um perfil de aço laminado w200 × 31,3. Determinar a tensão no ponto A: (a) para o carregamento mostrado;
Resolva o Prob. 4,114, considerando que a barra é substituída por um tupo de 20 mm de diâmetro externo e 16 mm de diâmetro interno.
Sabendo-se que a tensão admissível na seção ABD é 70 MPa, determinar a maior força P que pode ser aplicada ao suporte mostrado.
Um desvio h deve ser executado em uma barra circular maciça. Sabendo-se que a máxima tensão, depois desse desvio ser executado, não deve exceder três vezes a tensão na barra quando era reta, determina
Resolva o problema 4.112, assumindo que a carga de 20 kN é removida.