Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 4.Problemas - Ex. 183

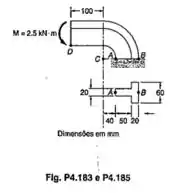
Um componente de máquina tem a seção transversal em forma de T , orientada como mostrado. Sabendo que M = 2500   N ⋅ m , determinar a tensão no (a) ponto A (b) ponto B

Passo 1

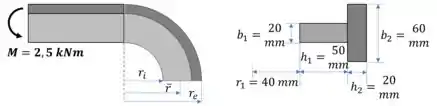
Primeiro vamos calcular o raio interno e externo da seção:

r i = 40   m m

r e = r i + h 1 + h 2 = 110   m m

Para resolver a questão, precisamos calcular o raio do centroide e o raio da linha neutra da seção, que são dados por:

r - = A 1 r 1 - + A 2 r 2 - A 1 + A 2

R = A 1 + A 2 b 1 ln ⁡ r e r i 1 + b 2 ln ⁡ r e r i 2

Vamos fazer uma tabela com as principais propriedades da seção transversal

r - = A 1 r 1 - + A 2 r 2 - A 1 + A 2 = 185000 2200 = 84,091   m m R = A 1 + A 2 b 1 ln ⁡ r e r i 1 + b 2 ln ⁡ r e r i 2 = 2200 28,2589 = 77,8517   m m e = r - - R = 6,2392   m m

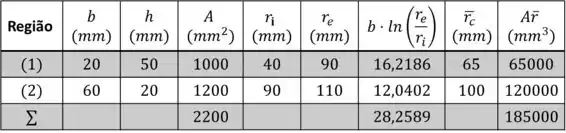
Passo 2

A tensão no ponto A é uma compressão:

σ A = M r i - R A e r 1

σ A = 2500   N m ⋅ 40   m m - 77,8517   m m 2200   m m 2 ⋅ 6,2392   m m ⋅ 40   m m

σ A = - 172,35   M P a

A tensão no ponto B é uma tração:

σ B = M r e - R A e r e

σ B = 2500   N m ⋅ 110   m m - 77,8517   m m 2200   m m 2 ⋅ 6,2392   m m ⋅ 110   m m

σ B = 53,23   M P a

Resposta

  1. σ A = - 172,35   M P a
  2. σ B = 53,23   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A porção curva da barra mostrada tem um raio interno de 7,6 mm. A linha de ação da força de 270 N está localizada a uma distância a do plano que contém o centro de curvatura da barra. Determinar a mai
Para a barra curva e o carregamento mostrado, determinar o percentual de erro introduzido no cálculo da tensão máxima, assumindo-se que a barra é reta. Considerar o caso quando: r = 5m m r = 25m m r =
Sabendo-se que a tensão admissível de compressão é 80M P a , determinar a maior distância a permissível da linha de ação da força de 270N , ao plano que contém o centro de curvatura da barra.
A porção curva da barra mostrada tem um raio interno de 7,6 mm. A linha de ação da força de 270 N está localizada a uma distância a do plano que contém o centro de curvatura da barra. Determinar a mai
A barra prismática curva tem uma seção transversal de 5 × 7,5m m e um raio interno de r 1 = 15m m . Para o carregamento mostradado, determinar as maiores tensões de tração e compressão