Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 11

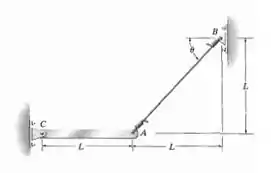
Se a carga aplicada à barra A C provocar o deslocamento do ponto A para a esquerda de uma quantidade ∆ L , determine a deformação normal no cabo A B . Originalmente, θ = 45 ° .

Passo 1

Fala aí galerinha, beleza? Bora pra mais uma questão. Esse problema vai exigir da gente muito mais conhecimentos de geometria do que de resmat. Então segura na minha mão, que a gente consegue!

A ideia aqui é que a gente precisa achar o comprimento final de A B depois da aplicação da força ( A ’ B ), para achar o valor da deformação, que vai ser dada por

ϵ = L A ' B - L A B L A b

Bora achar esse cara!

Passo 2

Antes da deformação, tínhamos algo assim:

Calculando a hipotenusa:

H = 2 L 2

H = L 2

Achamos nosso comprimento A B . Vamos seguir!

Passo 3

Após a aplicação da força para a esquerda, teremos um encurtamento da haste C A , o que nos dá algo como:

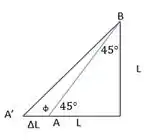
Onde o ângulo ∅ , do triângulo B A A ’ , pode ser determinado por:

∅ = 180 - 45 = 135 °

Passo 4

Ainda no mesmo triângulo, podemos determinar o lado A’B pela lei dos cossenos:

L A ' B = ∆ L 2 + L A B 2 - 2 ∆ L × L A B × cos ⁡ ∅

L A ' B = ∆ L 2 + 2 L 2 + 2 ∆ L L

Assim achamos A ' B . Portanto, a deformação será:

ε A B = L A ' B - L A B L A b = ∆ L 2 + 2 L 2 + 2 ∆ L L - 2 L L 2

Manipulando:

ε A B = 1 2 ∆ L L 2 + 1 + ∆ L L - 1

Resposta

ε A B = 1 2 ∆ L L 2 + 1 + ∆ L L - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O tubo rígido é sustentado por um pino em C e um cabo de ancoragem A B de aço A - 36 . Se o diâmetro do cabo for 5m m , determine a carga P se a extremidade B for deslocada 2,5m m para a direita.
Ao ser submetido a um ensaio de tração, um corpo de prova de liga de cobre com comprimento de referência de 50m m sofre uma deformação de 0,40m m / m m quando a tensão é de 490M P a . Se σ e =315M P a
O diâmetro da parte central do balão de borracha é d = 100 mm. Se a pressão do ar em seu interior provocar o aumento do diâmetro do balão até d = 125 mm, determine a deformação normal média na borrach
Se a deformação normal for definida em relação ao comprimento final, isto é: em vez de em relação ao comprimento original, mostre que a diferença entre essas deformações é representada como um termo d
Uma haste tem raio de 10mm . Se estiver sujeita a uma carga axial de 15N tal que a deformação axial na haste seja ϵ x = 2,75 ⋅ 10 - 6 , determine o módulo de elasticidade E e a mudança em seu diâmetro