Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 2.Problemas - Ex. 35

Se a deformação normal for definida em relação ao comprimento final, isto é:

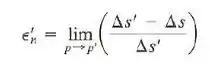
em vez de em relação ao comprimento original, mostre que a diferença entre essas deformações é representada como um termo de segunda ordem, a saber, ∈ n - ∈ ' n = ∈ n ∈ ' n .

Passo 1

Temos que provar que a diferença entre as transformações é dada por esta relação que o enunciado nos deu:

∈ n - ∈ ' n = ∆ S ' - ∆ S ∆ S - ∆ S ' - ∆ S ∆ S '

Aplicando produto notável, temos:

= ∆ S ' 2 - ∆ S ∆ S ' - ∆ S ' ∆ S + ∆ S 2 ∆ S ∆ S ' = ∆ S ' - ∆ S 2 ∆ S ∆ S '

Logo:

∈ n - ∈ ' n = ∆ S ' - ∆ S ∆ S ∆ S ' - ∆ S ∆ S ' = ∈ n ( ∈ ' n )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6.120 a 6.123 Para o dado estado plano de deformações usar o círculo de Mohr para determinar o estado de deformação associado aos eixos x'e y’, que foram girados de um ângulo θ , no sentido mostrado.
6.128 e 6.129 Em um ponto da superfície de uma placa fina foi determinado o estado de deformações. Sabendose que a superfície da placa está isenta de tensões e o coeficiente de Poisson é 0,30, determi
6.128 e 6.129 Em um ponto da superfície de uma placa fina foi determinado o estado de deformações. Sabendose que a superfície da placa está isenta de tensões e o coeficiente de Poisson é 0,30, determi
Um quadrado ABCD de 50mm de lado é riscado sobre a superfície de uma placa fina, quando a placa está sem carga. Depois da placa ser carregada, observou=se que os comprimentos dos lados AB e AD foram a
No P r o b . 6.100 , determinar o máximo valor admissível para h , sabendo-se que a tubulação é feita de um aço com uma tensão ultima a tração de 450M p a e que um coeficiente de segurança de 4,50 é d