Uma carga axial de será aplicada com uma excentricidade em uma barra circular de aço , que está livre em seu topo C e engastada em sua base . Sabendo-se que as barras disponíveis para o uso tem diâmetros desde até , em intervalos de , determinar a barra mais leve que pode ser usada se . Usar
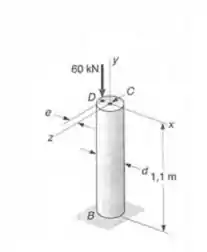
Passo 1
Então gurizada, vamos iniciar fazendo algumas conversões, para facilitar um pouco:
Passo 2
Agora, vamos a nossos cálculos:
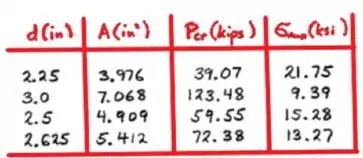
Usamos
Resposta
.