Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 55
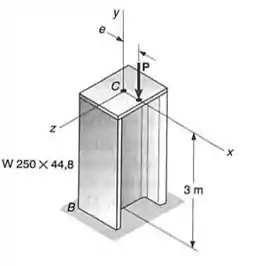
Uma carga axial P é aplicada em um ponto localizado sobre o eixo x a uma distância e= 12,7 mm do eixo geométrico do perfil laminado de aço w10 x 39 da coluna BC. Usando 200 GPa determinar a) carga P para que a deflexão horizontal do topo da coluna seja de 15 mm b) correspondente tensão máxima na coluna.
Passo 1
E ai gurizada tudo belezinha??? Vamos analisar a viga em questão... e vamos pegar algumas informações dessa viga no apêndice....
Para encontramos P vamos usar a equação abaixo...
Passo 2
Gurizada agora vamos encontrar a carga P para que a deflexão horizontal do topo da coluna seja de 15 mm
Isolando temos:
Passo 3
Agora sim podemos encontrar a tensão máxima, venha cmg!!!
Resposta
Exercícios de Livros Relacionados
Um elemento de aço com 5,8 m de comprimento de flambagem submetido à compressão deve suportar uma carga excêntrica P de 296 kN. Usando o método da interação, selecione o perfil de abas largas com 200
σ E = 345 M P a e E = 200 G P a .
10.114: Resolva o Problema 10.113 usando o método da interação, considerando que σ E = 344,8M P a e uma tensão admissível à flexão de 206,9 Mpa.(10.113)Uma coluna de aço com um comprimento de flambage
Uma coluna de aço com um comprimento de flambagem de 7,3 m é carregada excentricamente conforme mostra a figura. Usando o método da tensão admissível, selecione o perfil de mesa larga de 360 mm de alt
10.110: Resolva o Problema 10.109 considerando que e = 5,08m m . 2014 - T 6 para a qual a tensão admissível à flexão é de 165,5 Mpa. Usando o método da interação, determine a menor dimensão d da seção