Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 66
Uma carga axial de 60kN será aplicada com uma excentricidade e = 8mm em uma barra circular de aço BC, que está livre em seu topo C e engastada em sua base B. Sabendo-se que as barras disponíveis para uso tem diâmetros desde 40mm até 80mm, em intervalos de 4mm, determinar a barra mais leve que pode ser usada, se
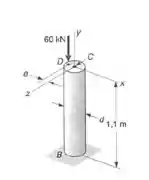
Passo 1
Galerinha, vamos ver os dados que temos para usarmos as fórmulas e realizar nosso cálculo:
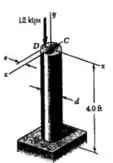
Passo 2
Agora partiu determinar a tensão D: usando o diâmetro abaixo
Resposta
Então gurizada, como acabamos de calcular, temos a resposta de
Exercícios de Livros Relacionados
Um membro de seção transversal retangular submetido à compressão, tem comprimento efetivo de 915mm e é feito da liga de alumínio 2014-T6, para a qual a tensão admissível é de 165 MPa. Usando o método
Resolver o prob. 144 assumindo que e= 5 mm
Um tubo retangular de aço é feito para suportar uma carga de 60kN, tendo uma excentricidade e=25mm. Os tubos disponíveis para o uso têm espessuras de parede que variam desde 6mm até 12mm, em increment
Uma coluna de madeira, de seção transversal retangular, tem um comprimento efetivo de 2,5m e deve suportar uma carga de 40kN, como mostrado. Usando o método da tensão admissível, projetar a coluna de
Resolver problema 148 selecionando o perfil laminado de aço de 250 mm de altura nominal