Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 69
Uma carga axial P de intensidade é aplicada em um ponto localizado sobre o eixo , a uma distância do eixo geométrico do perfil laminado de aço da coluna BC. Sabendo-se que a coluna está livre em seu topo C e engastada em suas base B e que e ,determine o coeficiente de segurança, em relação ao escoamento
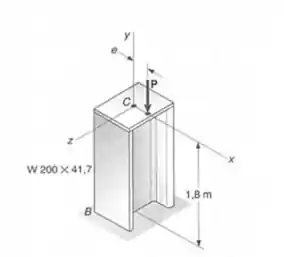
Passo 1
Vamos a nossos cálculos:
Para:
Usando 10,24 com e
Passo 2
Agora devemos determinar a deformação vem comigoo :D
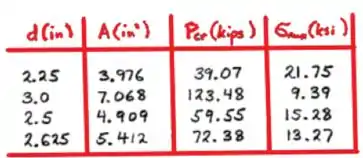
Usamos
Resposta
.
Exercícios de Livros Relacionados
10.40: Resolva o Prob. 10.39 assumindo que L é igual a 9,0m.(10.39)A linha de ação da força axial P é paralela ao eixo geométrico da coluna e é aplicada a um ponto localizado no eixo x à distância e =
10.42: Para o Problema 10.41, determine a distância d necessária para a qual a barra entrará em contato com o ponto C quando a temperatura aumentar em 120 ° F . 3 8 × 3 8 i n . De lado e é suspensa po
3 8 × 3 8 i n . De lado e é suspensa por pinos a uma distância fixa entre si e localizados a uma distância e = 0,03 i n . Do eixo geométrico da barra. Sabendo que na temperatura T 0 os pinos estão em
x à distância e = 12 m m do eixo geométrico da coluna B C de perfil de aço laminado W 310 × 60 . Assumindo que L = 7,0m e utilizado E = 200 G P a , determine (a) a carga P para a qual deflexão horizon
W 250 × 44,8 que está livre no topo C e engastada na base B. Sabendo que a excentricidade da força é e = 12 m m , e que para a classe do aço usado σ E = 250 M P aeE = 200 G P a , determine (a) a inten