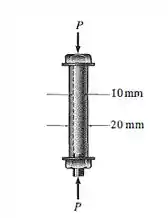
O parafuso de aço com de diâmetro está embutido em uma luva de bronze. O diâmetro externo dessa luva é e seu diâmetro interno é . Se o parafuso for submetido a uma força de compressão , determine a tensão normal média no aço e no bronze. , .

Vamos ver como as forças internas aparecem, montando o diagrama de corpo livre para uma seção do conjunto:

Lembre-se que a luva é um cilindro vazado, então aquele é pra representar a força em toda a luva.

Fazendo o equilíbrio de forças:

Duas incógnitas, mas apenas uma equação. Precisamos de mais uma!

Então, a gente pode pensar na equação de compatibilidade de deslocamento.

O nosso conjunto luva+corpo do parafuso está entre a cabeça do parafuso e a porca. A gente considera que essas duas coisas são rígidas, ou seja, não se deformam.

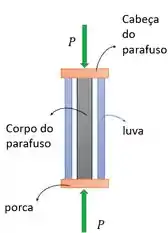
Como a cabeça do parafuso é rígida e a força é aplicada em seu centro, todos os pontos da cabeça desse parafuso descem igualmente por causa da carga. E o mesmo acontece para a porca, todos pontos dela sobem igualemente, conforme o corpo do parafuso e a luva se deformam.

Aí isso diz para gente que conjunto todo tem que comprimir o mesmo tamanho! Então o encurtamente do corpo do parafuso é igual ao encurtamente da luva:

Usando a fórmulinha da relação carga-deslocamento:

Substituindo ela na nossa equação da compatibilidade:

Simplificando a nossa equação:

Pronto, agora se substituirmos os valores, vamos achar uma relação entre e .

A área do parafuso é

A área da luva é

Susbtituindo isso e os outros dados:

Simplificando, chegamos em

Essa é a nossa segunda equação!

Agora é resolver o sisteminha e achar as forças que a gente precisa!

Substituindo o encontrado na primeira equação, que veio do balanço de forças:

E aí voltando na relação entre forças que saiu a compatibilidade, usando esse valor de :

Agora é usar a fórmulinha da tensão normal média em cada material:

Para o corpo do parafuso:

E para a luva: