Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 43
O parafuso tem diâmetro de 20 mm e passa por uma luva com diâmetro interno de e diâmetro externo de . O parafuso e a luva são feitos de aço e estão presos aos apoios rígidos como mostra a figura. Se o comprimento do parafuso for . e o comprimento da for luva for , determine a tração no parafuso quando for aplicada uma força de aos apoios.
Passo 1
Um parafuso está dentro de uma luva (um cilindro vazado) que conecta dois apoios. O conjunto todo está sendo forçado nas extremidades.
Características do parafuso:
- Diâmetro: . (Cilindro)
- Comprimento inicial: .
- Aço : (Tabelado)
Características da luva:
- Diâmetro interno: . Diâmetro externo: . (Cilindro vazado)
- Comprimento inicial: .
- Aço A-36: (Tabelado)
O forçamento é nas extremidades. E ocorre no parafuso e na luva!
Nós queremos descobrir a força interna que traciona o parafuso!
Passo 2
Vamos ver como aparece. Monte o diagrama de corpo livre para uma seção.
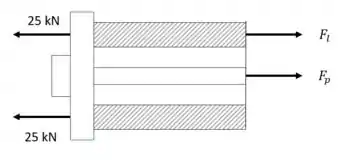
Lembre-se que a luva é um cilindro vazado, então aquele é pra representar a força em toda a luva (a posição vertical do vetor não importa aqui).
Equilíbrio de forças:
Duas incógnitas mas apenas uma equação. Vamos precisar de outra!
Passo 3
Esse tipo de exercício sempre se resume em ver qual é a condição de compatibilidade. A sacada aqui é reparar a luva e o parafuso têm que esticar o mesmo comprimento! Então
Use a fórmula da relação carga-deslocamento:
Pronto, agora se substituirmos os valores, vamos achar uma relação entre e !
A área do parafuso é .
A área da luva é .
Fazendo as contas na última equação chegamos em
Passo 4
Substitua o encontrado na primeira equação, que veio do balanço de forças:
Resposta
Tração no parafuso: .