Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 2.Problemas - Ex. 8

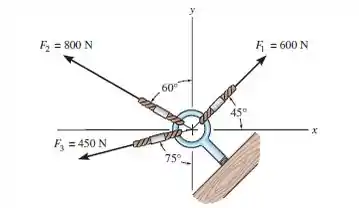
Determine a intensidade da força resultante F R = F 1 + F 2 e sua direção, medida no sentido horário a partir do eixo x positivo.

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a primeira questão de mais um livro juntos!

Nessa questão nós precisamos calcular a intensidade e a direção da força resultante obtida pela soma das forças F 1 e F 2 (Cuidado para não colocarem a força F 3 aí no meio).

Antes de tudo, vamos comemorar, pois a questão nos deu um sistema de coordenadas ortogonal (ângulos de 90° entre os eixos)!!! Tudo fica tão mais fácil aqui...

A forma mais fácil de resolvermos ambas as perguntas simultaneamente é escrevermos os vetores em termos das componentes em x e y . Para isto, vamos usar e abusar da trigonometria e da geometria do problema!

Passo 2

Vamos agora decompor os vetores F 1 e F 2 em relação as suas componentes x e y . Portanto,

F 1 x = F 1 cos ⁡ 45 ° = 424,3   N F 1 y = F 1 sen ⁡ 45 ° = 424,3   N

F 2 x = - F 2 sen ⁡ 60 ° = - 692,8   N F 2 y = F 2 cos ⁡ 60 ° = 400   N

Tomem muito cuidado aqui com relação aos ângulos utilizados e os sinais das componentes para que não errem ao decompor!

Passo 3

Agora que decompomos as duas forças já podemos realizar a soma delas.

Só que temos uma grande vantagem. Só podemos somar componente x com componente x (e o mesmo é válido para y ). Portanto,

F R x = F 1 x + F 2 x F R y = F 1 y + F 2 y ⟹ F R x = - 268,5   N F R y = 824,3   N

Como ambas as componentes são ortogonais, para obtermos a intensidade da força basta utilizarmos Pitágoras. Logo,

F R = - 268,5 2 + 824,3 2 = 866,9   N

E, para finalizarmos a questão, o ângulo ϕ entre a força e o eixo x medido no sentido horário é dado por:

ϕ = arctan ⁡ F R y F R x = arctan ⁡ 824,3 - 268,5 = 108 °

E agora sim finalizamos a questão!

Resposta

F R = 866,9   N

ϕ = 108 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o erro percentual n ao substituir-se o seno e tangente de um ângulo pelos valores do ângulo em radianos de 5 ° , 10 ° e 20 ° . Explique a diferença qualitativa entre os resultados de seno e
Para os vetores V 1 e V 2 do Prob. ½, determine o módulo da diferença vetorial V ' = V 2 - V 1 e o ângulo θ x que V ' faz com o eixo positivo x . Complete tanto a solução gráfica quanto a algébrica.
2.8. Se a força resultante precisa atuar ao longo do eixo u positivo e ter uma intensidade de 5k N , determine a intensidade necessária de F B e sua direção θ.
Demonstre: A B T = B T A T A B - 1 = B - 1 A - 1
Encontre a matriz de transformação que gira um sistema de coordenadas retangulares por um ângulo de 120 ° sobre um eixo que forma ângulos iguais com os três eixos de coordenadas originais.