Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 101
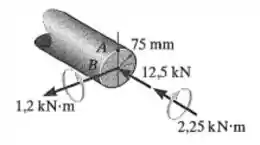
As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento de torção de 2,25 kN.m. Determine as tensões principais no ponto A. Calcule também a tensão de cisalhamento máxima no plano nesse ponto.
Passo 1
Falaa! Vamos entender o que ele quer. Ele pede as tensões principais no ponto .
Para achar essas fofas, precisamos achar o estado de tensões nesse ponto. (as tensões que acontecem nesse ponto). E depois calcular as principais através delas.
Ele já nos deu os esforços atuam na seção .
Momento torçor:
Momento fletor:
Força axial:
Vamos seguir!
Passo 2
Agora vamos achar as tensões em . A força axial vai causar compressão de:
Lembrando que a fórmula do momento de inércia de um círculo é dada por , onde é a distância do centro até a bora mais externa. Nosso momento de inércia vai ser:
A tensão normal dada pelo momento vai causar compressão também em . Ela é dada por
E é a distância do centro do tubo até o ponto , ou seja, o raio dele :
A tensão norma total é
Passo 3
Só vamos ter tensão cisalhante por causa da torção:
Substituindo nossos dados:
Uhul! Achamos todas as tensões no ponto .
Passo 4
Agora, é só achar as tensões principais no ponto pela fórmulinha:
Essa fórmula nos permite obter duas tensões, uma máxima e uma mínima .
Vimos que só temos uma tensão normal, e ela é de compressão:
Podemos colocar ela no lugar de ou , não vai fazer diferença. E temos uma tensão cisalhante:
Substituindo:
Logo:
Já a tensão cisalhante máxima será: