Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 97

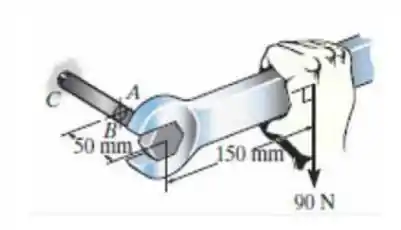
Resolva o Problema 9.96 para o ponto B.

Passo 1

Fala aí pessoal. O primeiro passo é determinar os esforços atuantes no ponto A. Transportando os esforços para o ponto B, teremos:

V = 90 N

T = 90 xx 0,15 = 13,5 N m

M = 90 xx 0,05 = 4,5 N m

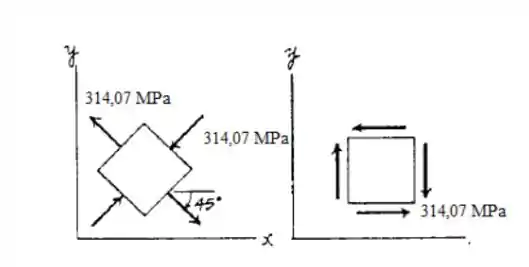
Logo, as tensões no ponto serão:

sigma_A = (M y)/(I) = 0

tau_B = (V Q)/(I t) - (T c)/(J) = - 314,066 M P a

Determinando as tensões principais, teremos:

sigma_1,2 = (sigma_x + sigma_y)/(2) +- sqrt(((sigma_x - sigma_y)/(2))^2 + (tau_x y)^2)

Logo, teremos:

sigma_1 = 314,066 M P a

sigma_2 = - 314,07 M P a

Portanto, podemos obter:

sigma_m á x = 314,07 M P a

sigma_i n t = 0

sigma_m í n = - 314,07 M P a

Passo 2

Com os dados obtidos, podemos obter os ângulos de orientação, que serão:

2 theta_p = 90 °

theta_p = 45 °

theta_s = 0 °

Além disso, podemos obter a tensão cisalhante máxima absoluta:

tau_a b s = (sigma_m á x - sigma_m í n)/(2) = 314,07 M P a

Por fim, basta mostrar os resultados finais:

Resposta

sigma_m á x = 314,07 M P a

sigma_i n t = 0

sigma_m í n = - 314,07 M P a

tau_a b s = 314,07 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar carga mostrada. (b) Determine os valores a serem esperados pa
Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar carga mostrada. (b) Determine os valores a serem esperados pa
Sabendo que σ a d m = 160M P a e τ a d m = 100M P a selecione o perfil de mesa larga mais econômico que deverá ser utilizado para suportar o carregamento mostrado. () Determine os valores a serem espe
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã
Os problemas a seguir, se referem a um perfil de aço laminado selecionado em um problema do capítulo 5, para suportar determinado carregamento a um custo mínimo e ao mesmo tempo satisfazendo a condiçã