Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 8.Problemas - Ex. 30

Resolva o Problema 8.29 considerando que 30   h p são transmitidos pela engrenagens G e 30   h p são transmitidos pela engrenagens H

Passo 1

E ai gurizada tudo bem? O enunciado pede para gente determinar o diâmetro, então vem comigo :D

60   h p = ( 60 ) ( 6600 ) = 396 × 10 3   i n / l b / s e g

f = 600   r p m 60   s e g / m i n -   10 �� H z

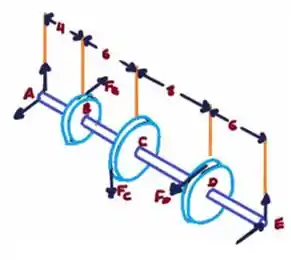
Passo 2

Força na engrenagem B:

T B = P 2 π f = 396 × 10 3 2 π ( 10 ) = 6302,5   l b / i n

Forças nas engrenagens C e D:

T C ´ = 40 60 T B = 3151,3   l b / i n

T D = 20 60 T B = 3151,3   l b / i n

Passo 3

Forças no eixo:

A B : T A B = 0 B C : T B C = 6302,5   l b / i n

C D : T C D = 3151,3   l b   i n . D E : T D E = 0

Forças da engrenagem:

F B = T B r B = 6302,5 3 = 2100,8   l b F C = T C r C = 3151,3   4 = 787,8   l b

F D = T B r B = 3151.3 4 = 787,8   l b

Passo 4

Considere os esforços abaixo para determinar os momentos ;)

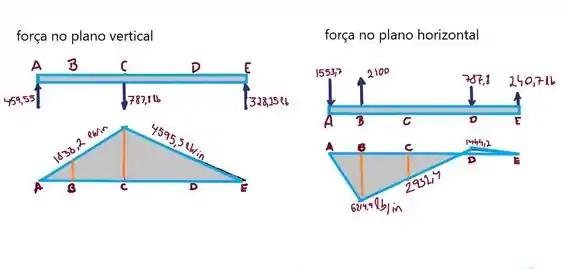
Em B + , M Y 2 + M Z 2 + T 2 = 1838,2 2 2 +   6214,9 2 2 +   6302,5 2 2 = 9040,2   l b / i n

Em C - , M Y 2 + M Z 2 + T 2 = 4595 , 5 2 +   2932 , 4 2 +   6302 , 5 2   =   8333,0   l b / i n

τ a l l = c J M Y 2 + M Z 2 + T 2 m a x J C = π 2 c 3 = M Y 2 + M Z 2 + T 2 τ a l l = 9040.3 8 × 10 3 = 1,1300   i n 3

c = 0,8960 i n . d = 2 c

d = 1.792   i n

Resposta

d = 1,792   i n .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

As cargas internas que agem sobre uma seção transversal no eixo de acionamento de uma turbina de 150 mm de diâmetro consistem em uma força axial de 12,5 kN, um momento fletor de 1,2 kN.m e um momento
A tensão em um ponto é mostrada no elemento. Determine as tensões principais e a tensão de cisalhamento máxima absoluta.
Resolva o Problema 9.96 para o ponto B.
Foi definido na Seção 8,2 que as tensões de cisalhamento produzidas em um eixo pelas cargas transversais são geralmente muito menores que aquela produzidas por torque . Nos Problema anteriores, seu ef
As duas de 2224k N são vertical e a força P é paralela ao eixo z . Sabendo que τ a d m = 55,2M P a . determine o menor diâmetro admissível para eixo cheio AE.