Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 103

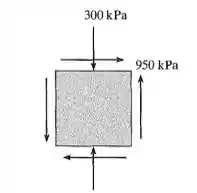
Determine o estado de tensão equivalente em um elemento se ele estiver orientado a 30º em sentido horário em relação ao elemento mostrado. Use as equações de transformação de tensão.

Passo 1

Fala aí pessoal. Vamos para a resolução de mais um probleminha de resmat. Este problema é bem curto e simples, basta substituir os valores dados nas fórmulas. Só temos que tomar cuidado para não confundirmos as fórmulas. Então vamos lá, as fórmulas são dadas por:

σ x ' = σ x + σ y 2 + σ x - σ y 2 cos ⁡ 2 θ + τ x y s e n ( 2 θ )

σ y ' = σ x + σ y 2 + σ x - σ y 2 cos ⁡ 2 θ + τ x y s e n ( 2 θ )

τ x ' y ' = - σ x - σ y 2 s e n ( 2 θ ) + τ x y c o s ( 2 θ )

Como o problema nos fornece as angulação e as tensões em x e y, basta substituir tais dados nas fórmulas. Os ângulos das fórmulas são os que o elemento faz com o eixo em questão, substituindo encontraremos:

σ x ' = - 0,898 M P a

σ y ' = 0,598 M P a

τ x ' y ' = 0,605 M P a

Resposta

σ x ' = - 0,898 M P a

σ y ' = 0,598 M P a

τ x ' y ' = 0,605 M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para os estados de tensão mostrados nas figuras, determine as tensões normal e de cisalhamento que atuam na face oblíqua do elemento triangular sombreado na figura. Use um método de análise com base n
Para os estados de tensão mostrados nas figuras, determine as tensões normal e de cisalhamento que atuam na face oblíqua do elemento triangular sombreado na figura. Use um método de análise com base n
Para os estados de tensão mostrados nas figuras, determine as tensões normal e de cisalhamento que atuam na face oblíqua do elemento triangular sombreado na figura. Use um método de análise com base n
Para o estado de tensões dado, determine (a) a orientação dos planos de máxima tensão de cisalhamento no plano de tensões e (b) a tensão normal correspondente.
Para o estado de tensões dado, determine as tensões normal e de cisalhamento depois que o elemento mostrado sofreu uma rotação de (a) 25 ° no sentido horário e (b) 10 ° no sentido anti-horário.