Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 53

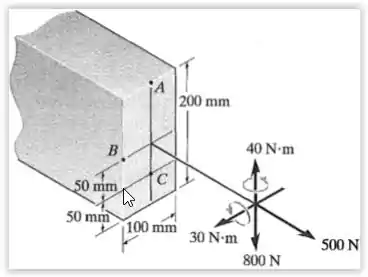
As cargas internas em uma seção da viga consistem em uma força axial de 500   N , uma força de cisalhamento de 800   N e duas componentes de momento 30   N ⋅ m e 40   N ⋅ m . Determine as tensões principais no ponto C . Calcule também a tensão de cisalhamento máxima nesse ponto.

Passo 1

Primeiro vamos calcular o momento de polar de inércia da seção transversal. Sabemos que para seções retangulares, temos a seguinte equação de momento de polar de inércia:

I = 1 12 ( b h 3 )

Onde b é o tamanho da parede paralela ao eixo e h é o tamanho da parede perpendicular ao eixo.

I x = 1 12 ( 0,1 × 0,2 3 )

∴ I x = 6,6667 × 10 - 5   m 4

Passo 2

Calcularemos da tensão no ponto C :

σ C = N z A + M x y C I x

σ C = 500   N ( 0,1 × 0,2 )   m 2 + ( 30   N ⋅ m ) ( 0,05   m ) 6,6667 × 10 - 5   m 4

σ B = 47,5   k P a   ( T r a ç ã o )

Passo 3

Cálculo da tensão máxima de cisalhamento no ponto C :

τ C = V y Q C I x t

τ C = ( 800   N ) ( 0 , 075 × 0 , 1 × 0 , 05   m 3 ) ( 6,6667 × 10 - 5   m 4 ) ( 0,1 m )

τ B = 45   k P a

Passo 4

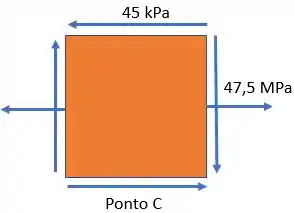
Calcularemos, então, as tensões principais no ponto C :

σ 1,2 = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

σ 1,2 = ( 47,5   k P a ) + ( 0   k P a ) 2 ± 47,5   k P a - ( 0   k P a ) 2 2 + ( - 45   k P a ) 2

σ 1,2 = 23,75   k P a ± 50,883   k P a

σ 1 = 74,6   k P a

σ 2 = - 27,1   k P a

Passo 5

Então, vamos calcular a tensão de cisalhamento máxima no plano τ m á x nesse ponto:

τ m á x = σ x - σ y 2 2 + τ x y 2

τ m á x = 47,5   k P a - 0   k P a ) 2 2 + ( - 45   k P a ) 2

τ m á x = 50,9   k P a

Resposta

As tensões principais no ponto C são:

σ 1 = 74,6   k P a

σ 2 = - 27,1   k P a

A tensão de cisalhamento máxima no plano é:

τ m á x = 50,9   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O eixo de seção cheia AB rotaciona a 600r p m e transmite 80k W a partir do motor M para a máquina-ferramentas conectadas à engrenagem F.Sabendo que τ a d m= 60M P a ,determine o menor diâmetro permit
O eixo de seção cheia ABC e as engrenagens mostradas na figura transmitem 10k W do motor M para uma máquina-ferramenta conectada à engrenages D . Sabendo que o motor gira 240r p m e que τ a d m = 60M
Resolva o Problema 8,25 considerando que o motor gira a 360r p m .
Resolva o Prob. 8.23 assumindo que o eixo AB rotacionado a 720r p m
O eixo cheio AE gira a 600r p m e transmite 60h p do motor M para as máquinas-ferramentas acopladas às engrenagens G e H .Sabendo que τ a d m= 55,2M P a e que 40h p são transmitidos pela engrenagens G