Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 4.Problemas - Ex. 21
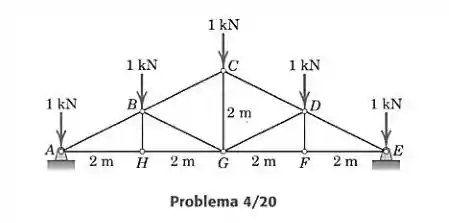
O carregamento do Prob. 4/19 é mosrado aplicado a um telhado em forma de treliça Howe. Despreze quaisquer reações horizontais nos apoios e determine as forças em todos os elementos. Compare com os resultados do Prob. 4/19.
Passo 1
Primeiro devemos analisar as força externas que atuam na treliça. Como ela é simétrica, as reações em e devem ser iguais e devem anular as forças externas verticais aplicadas. Então as forças pra cima nesses dois pontos são:
Passo 2
Agora, vamos resolver as equações de equilíbrio em e para cada nó, começando da esquerda. As forças positivas indicam tração e as negativas compressão, e sempre trataremos as forças desconhecidas como tração. Todas as barras inclinadas têm o mesmo ângulo com a horizontal. Temos:
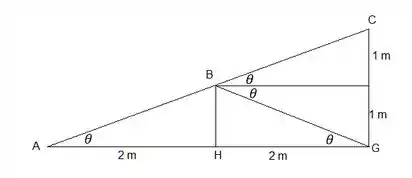
Sendo os catetos 1 m e 2 m, a hipotenusa mede:
E aí temos:
Passo 3
Nó A:
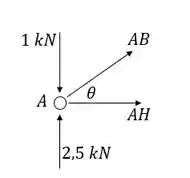
Substituindo na expressão de encontrada anteriormente:
Por simetria, obtemos também:
Passo 4
Nó H:
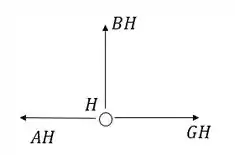
Podemos ver que nenhuma força é capaz de anular uma tração ou compressão vertical gerada por nesse ponto, então:
Além disso:
Por simetria, temos também:
Passo 5
Nó B:
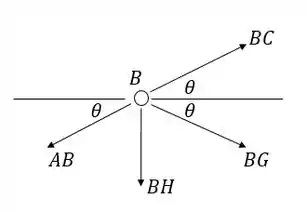
Dividindo tudo por achamos em função de :
Agora em :
Substituindo as forças e , achamos :
Agora achamos o valor de :
Por simetria, temos também:
Passo 6
No C:
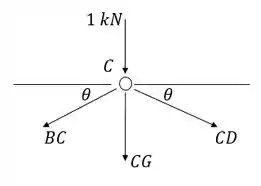
Substituindo os valores:
Resposta
Nesse caso as barras que não sofrem forças e poderiam ser retiradas são duas, e , e no Prob. 4/19 era só a barra .