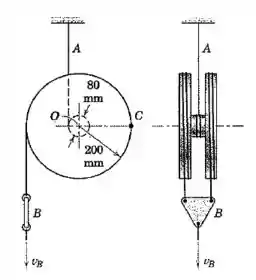
O carretel gira sobre seu cubo subindo o cabo interno enquanto a placa compensadora puxa os cabos externos para baixo. Os três cabos estão firmemente enrolados em torno de suas respectivas periferias e não deslizam. Se, no instante representado, tiver se deslocado para baixo uma distância de a partir do repouso com uma aceleração constante de , determine a velocidade do ponto e a aceleração do centro para esse instante em particular.

Vamos usar o método de inspeção de um deslocamento diferencial. Em outras palavras, vamos considerar um pequeno deslocamento e ver o que acontece no sistema.

(O desenho está bem fora de escala, para facilitar a visuaização)

E traçamos aquela reta azul de forma que cruze a reta horizontal preta no ponto fixo em torno do qual nosso sistema gira.

Agora podemos extrair algumas relações do nosso desenho. Usando semelhança de triângulos:

Em cada caso dividimos um deslocamento diferencial pela sua distância até o ponto fixo do movimento.

Vamos começar determinando a velocidade do ponto . Pela relação que escrevemos ali em cima:

Dividindo tudo por ficamos com:

Agora vamos procurar a aceleração do ponto . Mais uma vez, pela relação que escrevemos a partir do desenho:

Podemos dividir tudo por :

E derivando em relação ao tempo:

E a aceleração já foi dada no enunciado:

E tanto quando apontam no sentido vertical para cima, da forma como representamos no desenho.