Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 29
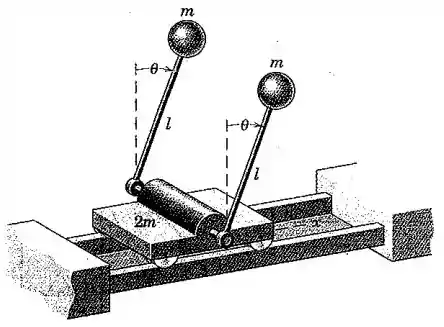
O carrinho de massa é livre para se mover ao longo dos trilhos horizontais e transporta as duas esferas, cada uma com massa , montadas sobre as hastes de comprimento e massa desprezível. O eixo ao qual as hastes são presas está montado no carrinho e é livre para girar. Se o sistema é liberado a partir do repouso com as hastes na posição vertical onde , determine a velocidade do carrinho e a velocidade angular das hastes no instante em que . Considere o carrinho e as esferas como partículas e despreze qualquer atrito.
Passo 1
Como não há atuação de forças externas na direção de , a quantidade de movimento se conservará nessa direção. Quando , as hastes estarão na vertical (para baixo), então a velocidade de rotação das esferas, de módulo , será inteiramente na direção , mas com sentido oposto.
Ou seja, o carrinho terá velocidade , mas as esferas terão velocidade :
Mais tarde, essa equação será útil.
Passo 2
Através da conservação de energia mecânica, podemos obter outra equação:
Sabendo que a energia cinética inicial é nula, temos:
Para o cálculo da variação de energia potencial gravitacional, consideremos o nível do carrinho como a altura zero:
Passo 3
Substituindo as expressões obtidas na equação de conservação de energia, obtemos:
No entanto, já sabemos que , logo,
E também: