Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.5 - Ex. 26
O pequeno carro, que possui uma massa de , se desloca livremente sobre o trilho horizontal e transporta a esfera de montada na haste leve que está girando com . Uma unidade motora mantém uma velocidade angular constante da haste. Se o carro possui uma velocidade quando , calcule quando . Despreze a massa das rodas e qualquer atrito.
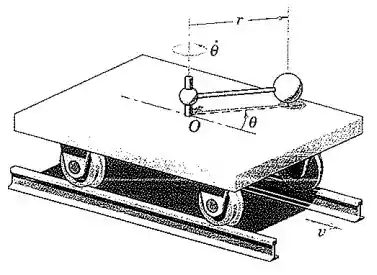
Passo 1
Como não há forças externas ao sistema na direção (mesma direção da velocidade ), a quantidade de movimento nessa direção não se alterará, de modo que:
Quando , a velocidade da esfera devida à rotação é perpendicular ao eixo , de modo que a única velocidade da esfera será . Sendo assim:
Passo 2
Quando , haverá uma componente da velocidade da esfera devida à rotação que estará na direção . Para nos ajudar a calcular essa componente, vamos olhar pra seguinte figura:
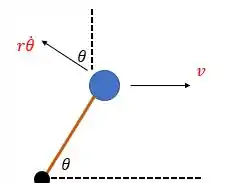
Aqui vemos que a componente da velocidade da esfera será:
Passo 3
Portanto, a quantidade de movimento final na direção será:
Igualando, obtemos: