Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 80
A hélice de um pequeno avião tem uma corrente de ar produzida de 2 m de diâmetro, gerando um empuxo de 4.000 N quando o avião está parado no solo. Considerando = 1,21 kg/m³ para o ar, determine (a) a velocidade do ar na corrente produzida, (b) o volume de ar que passa pela hélice por segundo, (c) a energia cinética transmitida por segundo para o ar na corrente produzida.
Passo 1
Vamos lá resolver mais essa? Quando a hélice do avião se movimenta, em um certo intervalo de tempo, forma um cilindro imaginário, como mostra a figura abaixo:
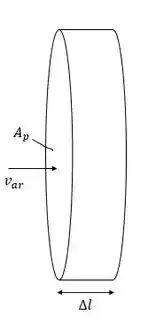
Assim, a força de empuxo da hélice pode ser calculada por:
Onde é a velocidade a jusante e é a velocidade a montante, que pode ser desprezada para esse caso. O cálculo de dm/dt pode ser feito como:
Passo 2
Com uma expressão para calcular a taxa de variação de massa, podemos calcular a velocidade de ar à jusante:
E com isso podemos calcular a vazão de ar que passa pela hélice:
Passo 3
A energia cinética por segundo gerada pela corrente de ar é calculada por:
Resposta
- 32,4 m/s
- 101,16 m³/s
- 64,6 kJ/s