Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas de Revisão - Ex. 110

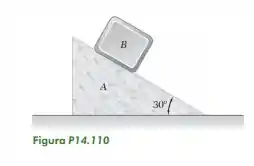
14.110. Um bloco de 9 kg parte do repouso e desce deslizando sobre a superfície inclinada de uma cunha A de 15 kg que está apoiada sobre uma superfície horizontal. Desprezando o atrito, determine (a) a velocidade do bloco B em relação à cunha A após ele ter deslizado 0,6 m sobre a superfície da cunha, (b) a velocidade correspondente da cunha.

Passo 1

Vamos matar mais uma?

Bom, no começo do movimento o sistema está em repouso, o que significa que o momento linear inicial é nulo, já no final do movimento tanto o A quanto B possui velocidade.

Podemos começar usando princípio impulso-momento:

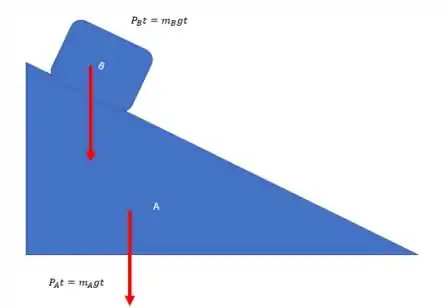
E depois fica

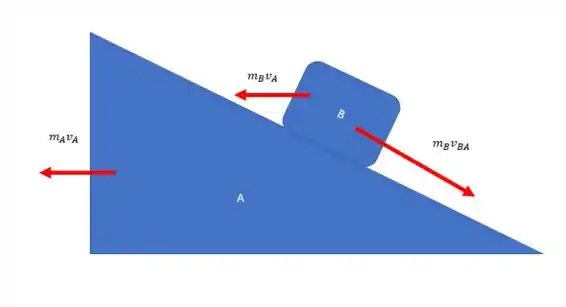
Então

∑ m v 0 + ∑ F t = ∑ m v f

Passo 2

Vamos fazer separadamente para cada componente, para a componente x, temos

0 = m B v B A cos ⁡ 30 ° - m A v A - m B v A

Vamos isolar v A

0 = m B v B A cos ⁡ 30 ° - v A m A + m B

v A = m B cos ⁡ 30 ° m A + m B v B A

Substituindo os valores v A = 9 ⋅ cos ⁡ 30 ° 15 + 9 v B A = 0,32476   v B A

Passo 3

Agora podemos usar conservação de energia.

∑ T i + V i = ∑ T f + V f

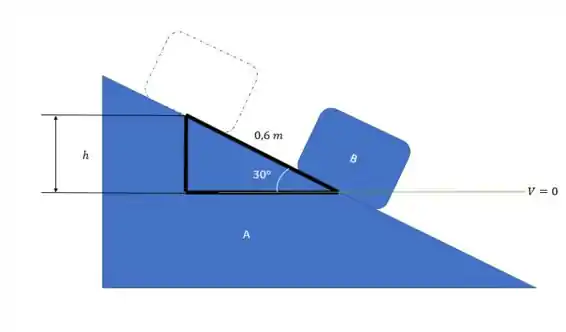
Então

0 + m B g h = 1 2 m A v A 2 + 1 2 m B v B 2

Como podemos ver na figura

h = 0,6 ⋅ sin ⁡ 30 °

Se olharmos as velocidades podemos ver outro triangulo:

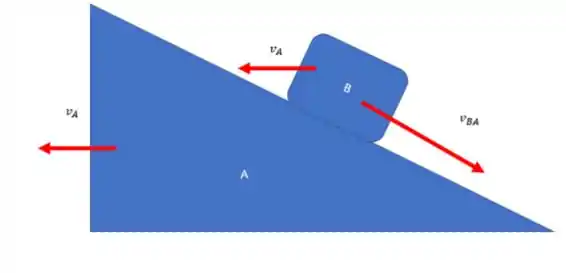
Disso tiramos

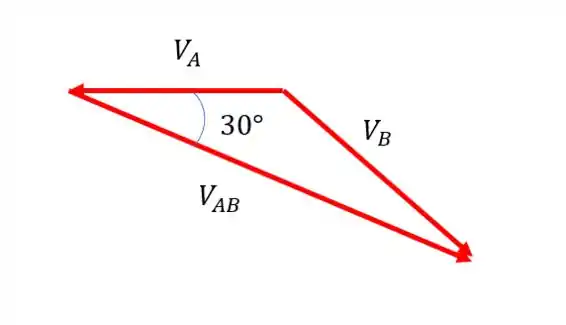
Basta mudar os vetores de lugar um pouquinho. Então, se usarmos o teorema dos cossenos:

v B 2 = v A 2 + v B A 2 - 2 v A v B A cos ⁡ 30 °

Então nossa equação fica:

m B g h = 1 2 m A v A 2 + 1 2 m B v A 2 + v B A 2 - 2 v A v B A cos ⁡ 30 °

Substituindo os valores que conhecemos

9 9,81 0,6 sin ⁡ 30 ° = 1 2 15 0,32476   v B A 2 + 1 2 9 [ 0,32476   v B A 2 + v B A 2 - 2 0,32476   v B A v B A cos ⁡ 30 °

Isso tudo aqui fica

26,87 = 3,2344 v B A 2

Logo

v B A = 2,86 m s

E como vemos na imagem, sua inclinação é - 30 ° em relação ao eixo x positivo.

E essa é a resposta do item (a).

Passo 4

Esse aqui vai ser rapidinho, porque lá no comecinho a gente já definiu uma expressão para v A , lembra?

v A = 0,32476   v B A

Então

v A = 0,32476 2,86 = 0,929 m s  

Mas como v A está para a esquerda, essa velocidade é negativa, então

v A = - 0,929 m s

Resposta

a v B A = 2,86 m s ; θ = - 30 ° b v A = - 0,929 m s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um motociclista se move com uma velocidade escalar vd constante ao longo de uma trajetória. Onde em um pequeno trecho assume uma forma de curva senoidal. Determinar as componentes x e y da velocidade,
No instante mostrado, o carro A move-se ao longo da porção reta da estrada com uma velocidade escalar de 25 m/s. Neste mesmo instante, o carro B move-se ao longo da porção circular da estrada com uma
A posição de uma partícula é definida por r = t 3 i → + 2 t 2 j → + 8 t k →m , onde t é dado em segundos. Determine a intensidade da velocidade e da aceleração e o raio de curvatura da trajetória quan
A posição de uma partícula é definida por r = 2 sen ⁡ π 4 t i → + 2 cos ⁡ π 4 t j → + 3 t k →m , onde t é dado em segundos. Determine as intensidades da velocidade e da aceleração em qualquer instante
A velocidade de uma partícula é dada por v = 16 t 2 i + 4 t 3 j + 5 t + 2 k m/s, onde t é dado em segundos. Se a partícula está na origem quando t = 0 , determine a intensidade da aceleração da partíc