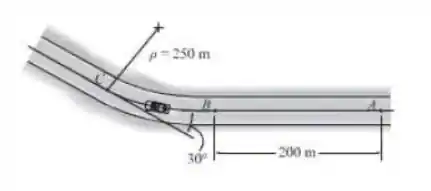
Quando o carro chega ao ponto A, ele tem velocidade escalar de . Se os freios são acionados, sua velocidade escalar é reduzida em . Determine a intensidade da aceleração do carro imediatamente antes de ele chegar ao ponto C.

Vamos começar por determinar as funções que governam a velocidade e a posição do carro. Partindo pela definição, temos:

Já para a posição, temos:

Agora, temos todas as funções necessárias para resolvermos a questão.

Para descobrirmos o tempo necessário para sair do ponto A até o ponto C, vamos utilizar a fórmula da posição. Mas, para isto, precisamos calcular antes esta distância. Sabemos então que,

Como , pois é um segmento reto, só nos falta obter . Assumindo que este segmento é um arco de circunferência, sabemos então que:

E ficamos neste questionamento de quem é . Este ângulo nada mais é do que os 30° na figura da questão! Sendo assim, passando para radianos (não podem esquecer deste passo de jeito nenhum!!!!!), teremos:

Portanto, o comprimento é

Vamos determinar agora o tempo . Para isto, precisamos resolver a seguinte equação:

Esta não é uma equação que conseguimos resolver facilmente. Para isto, vamos utilizar algum software para nos ajudar nesta solução. Montando uma tabela para podermos descobrir o intervalo em que se encontra, temos:

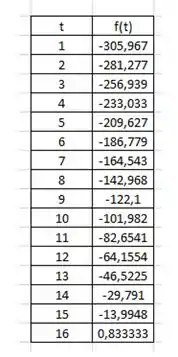
Como podemos observar na tabela acima, o valor do tempo está entre 15 e 16, e muito mais próximo de 16. Vamos montar outra tabela com variações dentro deste intervalo. Sendo assim, temos:

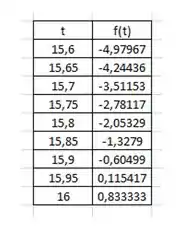
Na tabela acima, percebemos que a nossa solução está no intervalo de 15,9 até 15,95. Vamos assumir um valor aproximado para a solução, dizendo que , pois é o valor mais próximo de zerar a nossa equação.

Agora podemos calcular todos os dados que faltavam. Determinando a velocidade do carro, temos:

Já para as componentes da aceleração, temos:

Por fim, a intensidade da aceleração do carro é: