Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 138
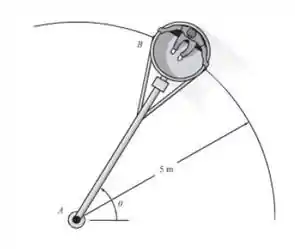
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de , onde é dado em segundos. Se um carro parte do repouso quando , determine as intensidades da sua velocidade e aceleração quando o braço AB gira . Despreze a dimensão do carro.
Passo 1
Para podermos calcular a velocidade e as componentes da aceleração precisamos determinar o tempo necessário para o carro chegar ao ponto B, pois todas as equações da cinemática estão em função do tempo, neste caso. Para isto, precisamos utilizar as equações na sua forma integral para obter a função da posição. Depois, descobriremos o tempo necessário para chegar ao ponto B.
Só nos fica um questionamento. Qual é o comprimento para chegar ao ponto B??? Basta lembrar que a curva percorrida é um arco de circunferência! Portanto, basta fazer a seguinte conta:
Simples, né?!? Agora, depois de obter o , basta fazer o caminho inverso!
Passo 2
Vamos obter as funções da velocidade e da posição. Para isto, vamos começar integrando a função da aceleração tangencial.
Já para a posição, temos:
Passo 3
Agora, precisamos descobrir o quando o carro percorreu após uma rotação de . Calculando o comprimento deste arco temos:
Portanto, temos que descobrir o tempo para que . Esta é uma equação que não conseguimos uma solução exata. Podemos utilizar quaisquer artifícios para a solução: soluções numéricas, softwares, análise do gráfico, etc. Resolvendo-o, descobrimos que o valor de é aproximadamente .
Agora que descobrimos o tempo, podemos calcular os parâmetros da questão!
Passo 4
Vamos determinar inicialmente a velocidade do carro. Substituindo o valor na sua equação, obtemos:
Já os termos da aceleração são dados por:
Portanto, a magnitude da aceleração é: